1 Random number generation

The stochastic integration methods of the last section took it for granted that we can produce random numbers from various distributions. Actually, we can’t. The best that can be done is to produce a completely deterministic sequence of numbers which appears indistinguishable from a random sequence with respect to any relevant statistical property that we choose to test. In other words, we may be able to produce a deterministic sequence of numbers that can be very well modelled as being a random sequence from some distribution. Such deterministic sequences are referred to as sequences of pseudorandom numbers, but the pseudo part usually gets dropped at some point.

The fundamental problem, for our purposes, is to generate a pseudorandom sequence that can be extremely well modelled as a sequence of realizations of i.i.d. \(U(0,1)\) random variables. Given such a sequence, it can be straightforward to generate deviates from other distributions, but the i.i.d. \(U(0,1)\) generation is where one problem lies. Indeed if you read around this topic then most books will pretty much agree about how to turn uniform random deviates into deviates from a huge range of other distributions, but advice on how to get the uniform deviates in the first place is much less consistent.

1.1 Simple generators and what can go wrong

Since the 1950s there has been much work on linear congruential generators. The intuitive motivation is something like this. Suppose I take an integer, multiply it by some enormous factor, re-write it in base - ‘something huge’, and then throw away everything except for the digits after the decimal point. Pretty hard to predict the result, no? So, if I repeat the operation, feeding each step’s output into the input for the next step, a more or less random sequence might result. Formally, the pseudorandom sequence is defined by \[ X_{i+1} = a X_i + b ~ ({\rm mod} ~M) \] where \(b\) is 0 or 1, in practice. This is started with a seed \(X_0\). The \(X_i\) are integers (\(<M\), of course), but we can define \(U_i = X_i/M\). Now the intuitive hope that this recipe might lead to \(U_i\) that are reasonably well modelled by i.i.d. \(U(0,1)\) r.v.s is only realised for some quite special choices of \(a\) and \(M\), and it takes some number theory to give the generator any sort of theoretical foundation (see Ripley, 1987, Chapter 2).

An obvious property to try to achieve is full period. We would like the generator to visit all possible integers between \(1-b\) and \(M-1\) once before it starts to repeat itself (clearly the first time it revisits a value, it starts to repeat itself). We would also like successive \(U_i\)s to appear uncorrelated. A notorious and widely used generator called RANDU, supplied at one time with IBM machines, met these basic considerations with \[ X_{i+1} = 65539 X_i ~ ({\rm mod} ~ 2^{31}) \] This appears to do very well in 1 dimension.

n <- 100000 ## code NOT for serious use
x <- rep(1,n)
a <- 65539;M <- 2^31;b <- 0 ## Randu
for (i in 2:n) x[i] <- (a*x[i-1]+b)%%M
u <- x/(M-1)
qqplot((1:n-.5)/n,sort(u))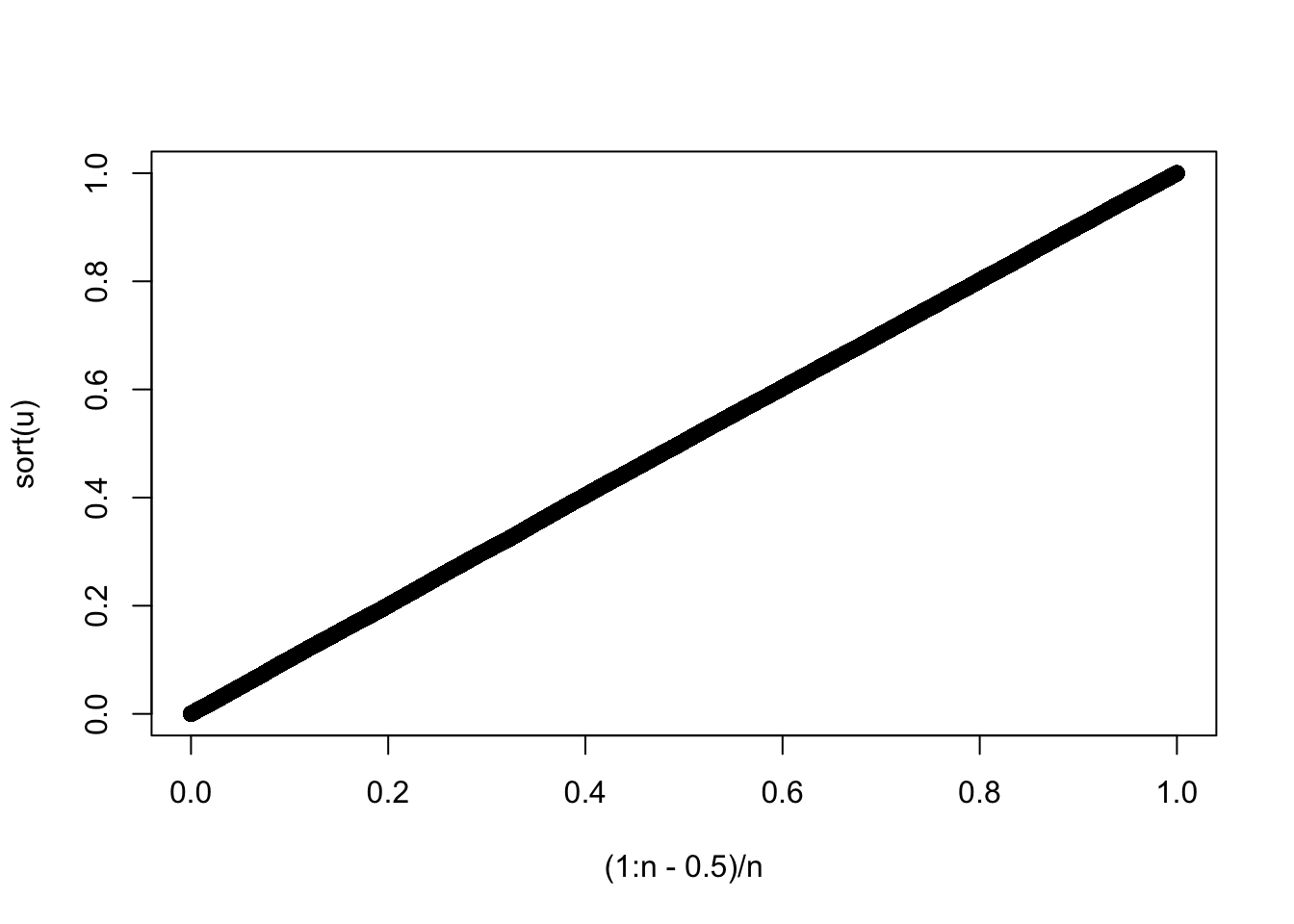

Similarly a 2D plot of \(U_i\) vs \(U_{i-1}\) indicates no worries with serial correlation

## Create data frame with U at 3 lags...
U <- data.frame(u1=u[1:(n-2)],u2=u[2:(n-1)],u3=u[3:n])
plot(U$u1,U$u2,pch=".")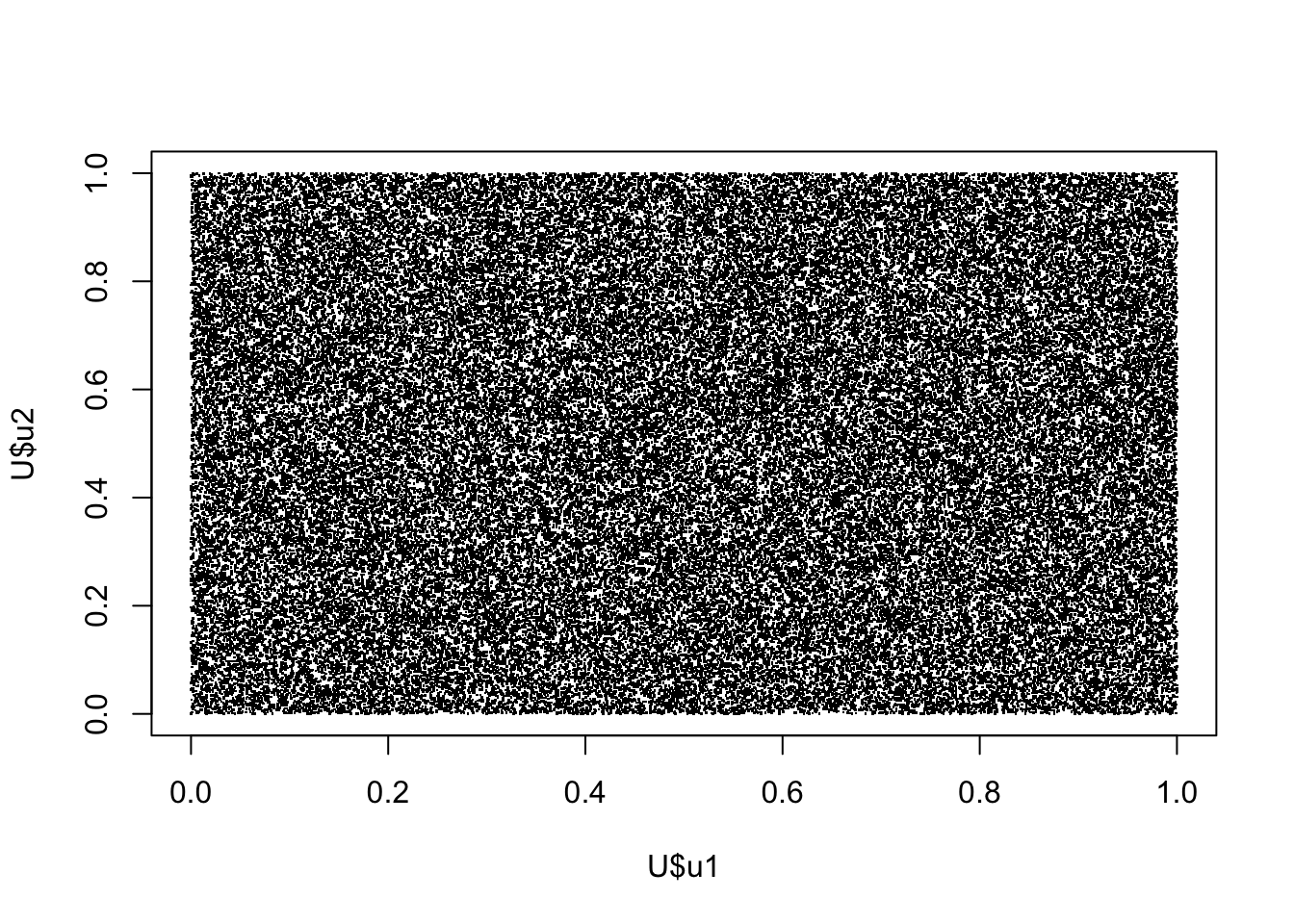

We can also check visually what the distribution of the triples \((U_i, U_{i-1},U_{i-2})\) looks like.

library(lattice)
cloud(u1~u2*u3,U,pch=".",col=1,screen=list(z=40,x=-70,y=0))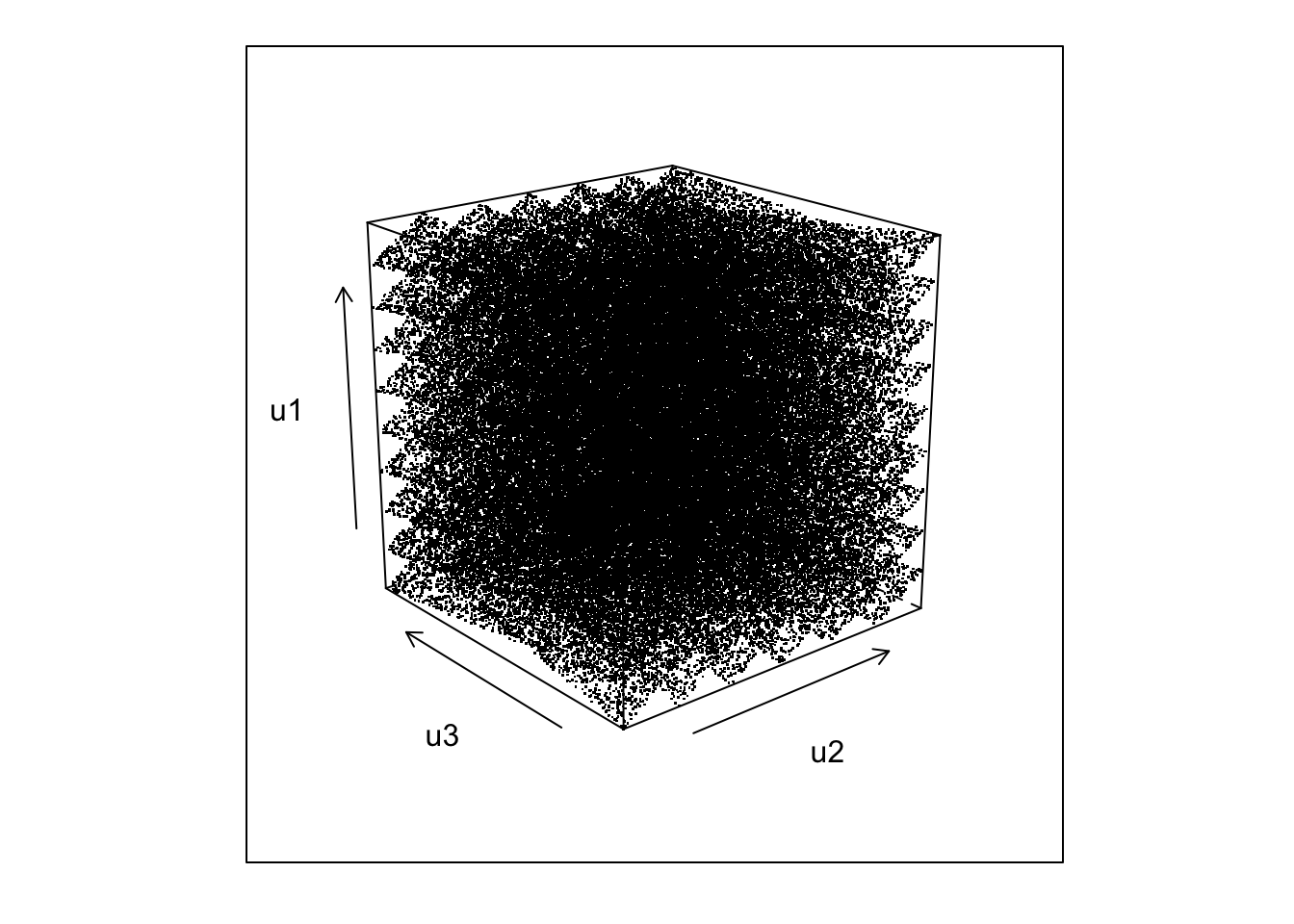

not quite so random looking. Experimenting a little with rotations gives

cloud(u1~u2*u3,U,pch=".",col=1,screen=list(z=40,x=70,y=0))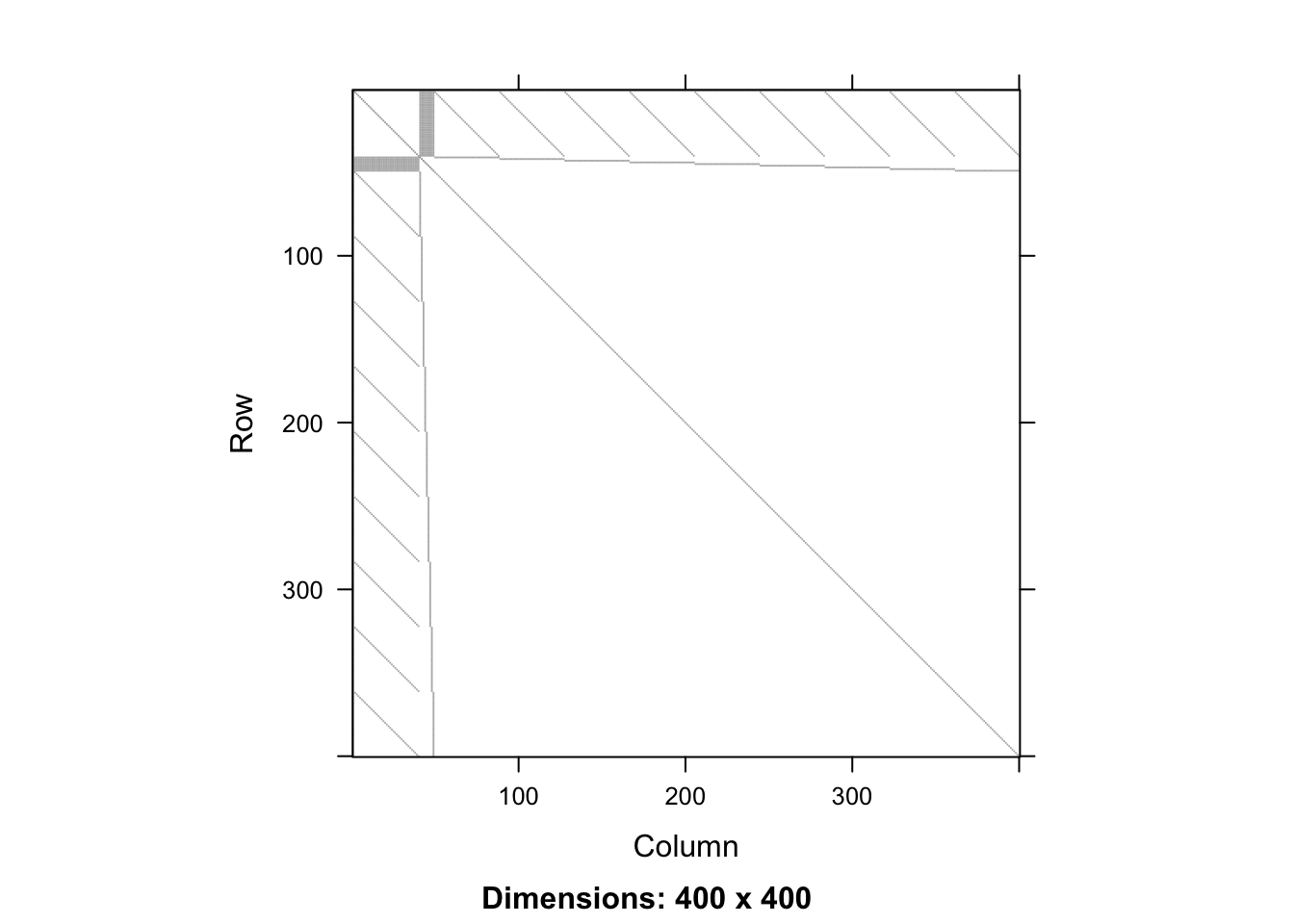

i.e. the triples lie on one of 15 planes. Actually you can show that this must happen (see Ripley, 1987, section 2.2).

Does this deficiency matter in practice? When we looked at numerical integration we saw that quadrature rules based on evaluating integrands on fixed lattices become increasingly problematic as the dimension of the integral increases. Stochastic integration overcomes the problems by avoiding the biases associated with fixed lattices. We should expect problems if we are performing stochastic integration on the basis of random numbers that are in fact sampled from some coarse lattice.

So the first lesson is to use generators that have been carefully engineered by people with a good understanding of number theory, and have then been empirically tested (Marsaglia’s Diehard battery of tests provides one standard test set). For example, if we stick with simple congruential generators, then \[ X_i = 69069 X_{i-1}+1 ~ ({\rm mod} ~2^{32}) \tag{1}\] is a much better bet. Here is its triples plot. No amount of rotating provides any evidence of structure.

Although this generator is much better than RANDU, it is still problematic. An obvious infelicity is the fact that a very small \(X_i\) will always be followed by an unusually small \(X_{i+1}\) (consider \(X_i = 1\), for example). This is not a property that would be desirable in a time series simulation, for example. Not quite so obvious is the fact that for any congruential generator of period \(M\), then \(k-\)tuples, \(U_i, U_{i-1}, \ldots, U_{i-k+1}\) will tend to lie on a finite number of \(k-1\) dimensional planes (e.g. for RANDU we saw 3-tuples lying on 2 dimensional planes.) There will be at most \(M^{1/k}\) such planes, and as RANDU shows, there can be far fewer. The upshot of this is that if we could visualise 8 dimensions, then the 8-tuple plot for Equation 1 would be just as alarming as the 3D plot was for RANDU. 8 is not an unreasonably large dimension for an integral.

Generally then, it might be nice to have generators with better behaviour than simple congruential generators, and in particular we would like generators where \(k-\)tuples appear uniformly distributed on \([0,1]^k\) for as high a \(k\) as possible (referred to as having a high k-distribution}).

1.2 Building better generators

An alternative to the congruential generators are generators which focus on generating random sequences of 0s and 1s. In some ways this seems to be a natural representation of numbers when using modern digital computers. One family of generators are those often termed shift-register generators. The basic approach is to use bitwise binary operations to make a binary sequence `scramble itself’. An example is Marsaglia’s (2003) Xorshift generator as recommended in Press et al. (2007).

Let \(x\) be a 64-bit variable (i.e. an array of 64 0s or 1s). The generator is initialised by setting to any value (other than 64 0s). The following steps then constitute one iteration (update of \(x\)) \[\begin{eqnarray*} x &\leftarrow& x \wedge (x \gg a) \\ x &\leftarrow& x \wedge (x \ll b) \\ x &\leftarrow& x \wedge (x \gg c) \end{eqnarray*}\] each iteration generates a new random sequence of 0s and 1s. \(\wedge\) denotes `exclusive or’ (XOR) and \(\gg\) and \(\ll\) are right-shift and left shift respectively, with the integers \(a, b\) and \(c\) giving the distance to shift. \(a=21\), \(b=35\) and \(c=4\) appear to be good constants (but see Press et al., 2007, for some others).

If you are a bit rusty on these binary operators then consider an 8-bit example where x=10011011 and z=01011100.

x<<1 is 00110110, i.e. the bit pattern is shifted leftwards, with the leftmost bit discarded, and the rightmost set to zero.
x<<2 is 01101100, i.e. the pattern is shifted 2 bits leftwards, which also entails discarding the 2 leftmost bits and zeroing the two rightmost.
x>>1 is 01001101, same idea, but rightwards shift.
x^z is 11000111, i.e. a 1 where the bits in x and z disagree, and a 0 where they agree.

The Xorshift generator is very fast, has a period of \(2^{64}-1\), and passes the Diehard battery of tests (perhaps unsurprising as Marsaglia is responsible for that too). These shift register generators suffer similar granularity problems to congruential generators (there is always some \(k\) for which \([0,1]^k\) can not be very well covered by even \(2^{64}-1\) points), but tend to have all bit positions `equally random’, whereas lower order bits from congruential generator sequences often have a good deal of structure.

Now we reach a fork in the road. To achieve better performance in terms of longer period, larger k-distribution, and fewer low order correlation problems, there seem to be two main approaches, the first pragmatic, and the second more theoretical.

Combine the output from several ‘good’, well understood, simple generators using operations that maintain randomness (e.g. XOR and addition, but not multiplication). When doing this, the output from the combined generators is never fed back into the driving generators. Preferably combine rather different types of generator. Press et al. (2007) make a convincing case for this approach. Wichmann-Hill, available in R is an example of such a combined generator, albeit based on 3 very closely related generators.
Use more complicated generators — non-linear or with a higher dimensional state that just a single \(X_i\) (see Gentle, 2003). For example, use a shift register type generator based on maintaining the history of the last \(n\) bit-patterns, and using these in the bit scrambling operation. Matsumoto and Nishimura’s (1998) Mersenne Twister is of this type. It achieves a period of \(2^{19937}-1\) (that’s not a misprint: \(2^{19937}-1\) is a ‘Mersenne prime’ (numbers this large are often described as being `astronomical’, but this doesn’t really do it justice: there are probably fewer than \(2^{270}\) atoms in the universe), and is 623-distributed at 32 bit accuracy. i.e. its 623-tuples appear uniformly distributed (each appearing the same number of times in a full period) and spaced \(2^{-32}\) apart (without the ludicrous period this would not be possible). It passes Diehard, is the default generator in R, and C source code is freely available.

1.3 Uniform generation conclusions

I hope that the above has convinced you that random number generation, and use of pseudo-random numbers are non-trivial topics that require some care. That said, most of the time, provided you pick a good modern generator, you will probably have no problems. As general guidelines

Avoid using black-box routines supplied with low level languages such as C, you don’t know what you are getting, and there is a long history of these being botched.
Do make sure you know what method is being used to generate any uniform random deviates that you use, and that you are satisfied that it is good enough for purpose.
For any random number generation task that relies on \(k-\)tuples having uniform distribution for high \(k\) then you should be particularly careful about what generator you use. This includes any statistical task that is somehow equivalent to high dimensional integration.
The Mersenne Twister is probably the sensible default choice in most cases, at present. For high dimensional problems it remains a good idea to check answers with a different high-quality generator. If results differ significantly, then you will need to find out why (probably starting with the `other’ generator).

Note that I haven’t discussed methods used by cryptographers. Cryptographers want to use (pseudo)random sequences of bits (0s and 1s) to scramble messages. Their main concern is that if someone were to intercept the random sequence, and guess the generator being used, they should not be able to infer the state of the generator. Achieving this goal is quite computer intensive, which is why generators used for cryptography are usually over engineered for simulation purposes.

1.4 Other deviates

Once you have a satisfactory stream of i.i.d. \(U(0,1)\) deviates then generating deviates from other standard distributions is much more straightforward. Conceptually, the simplest approach is inversion. We know that if \(X\) is from a distribution with continuous c.d.f. \(F\) then \(F(X)\sim U(0,1)\). Similarly, if we define the inverse of \(F\) by \(F^-(u) = {\rm min}(x|F(x)\ge u)\), and if \(U\sim U(0,1)\), then \(F^-(U)\) has a distribution with c.d.f. \(F\) (this time with not even a continuity restriction on \(F\) itself).

As an example here is inversion used to generate 1 million i.i.d. \(N(0,1)\) deviates in R.

system.time(X <- qnorm(runif(1e6)))

   user  system elapsed 
  0.018   0.001   0.019

For most standard distributions (except the exponential) there are better methods than inversion, and the happy situation exists where textbooks tend to agree what these are. Ripley’s (1987) Chapter 3 is a good place to start, while the lighter version is provided by Press et al. (2007) Chapter 7. R has many of these methods built in. For example an alternative generation of 1 million i.i.d. \(N(0,1)\) deviates would use.

system.time(Z <- rnorm(1e6))

   user  system elapsed 
  0.024   0.001   0.025

Here the difference is marginal, due to the highly optimized qnorm function in R, but for other distributions the difference can be substantial.

We have already seen how to generate multivariate normal deviates given i.i.d. \(N(0,1)\) deviates, and for other (simple) multivariate distributions see chapter 4 of Ripley (1987). For more complicated distributions see the Computationally-Intensive Statistical Methods APTS module.

2 An example: sparse matrix computation

Many statistical computations involve matrices which contain very high proportions of zeroes: these are known as sparse matrices. Most of the computational time used by most numerical linear algebra routines is devoted to additions, subtractions and multiplications of pairs of floating point numbers: if we know, in advance, that one of the pair is a zero, we don’t actually need to perform the operation, since the answer is also known in advance. In addition, there is little point in storing all the zeroes in a sparse matrix: it is often much more efficient to store only the values of the non-zero elements, together with some encoding of their location in the matrix.

Efficient storage and simple matrix manipulations are easy to implement. Here is an example, based on simulating the model matrix for a linear model with 2 factors, and a large number of observations.

  n <- 100000 ## number of obs
  pa <- 40;pb <- 10 # numbers of factor levels
  a <- factor(sample(1:pa,n,replace=TRUE))
  b <- factor(sample(1:pb,n,replace=TRUE))
  X <- model.matrix(~a*b) # model matrix a + b + a:b
  y <- rnorm(n) # a random response
  object.size(X) # X takes lots of memory!

326428560 bytes

  sum(X==0)/prod(dim(X)) # proportion of zeros

[1] 0.9906194

so the simulated \(\bf X\) is \(100,000 \times 400\) and is about 99% zeroes. It requires about 0.3Gb of computer memory, if stored as a normal ‘dense’ matrix. The Matrix library, supplied with R, supports sparse matrix computations, so the following produces a sparse version of \(\bf X\)

par(mar=c(4,4,1,1))

library(Matrix)
Xs <- Matrix(X) ## a sparse version of X
## much reduced memory footprint
as.numeric(object.size(Xs))/as.numeric(object.size(X))

[1] 0.03348825

Because Xs doesn’t store the zeroes, it uses much less memory than the dense version X. Note that although X is only 1% non-zeroes, Xs uses 3% of the storage of X, because it needs to store the locations of the non-zero elements, in addition to their values. The sparse approach also saves computer time when performing basic matrix operations, by avoiding the floating point operations that are not needed because they involve a zero. For example

system.time(Xy <- t(X)%*%y)

   user  system elapsed 
  0.085   0.026   0.110

system.time(Xsy <- t(Xs)%*%y)

   user  system elapsed 
  0.003   0.001   0.004

Again computational overheads involved in only storing the non-zeroes, and their locations, means that the cost of the sparse operation is more than 1% of the dense cost, but the saving is still substantial.

Any competent programmer could produce code for the examples given so far, but any serious application will involve solving linear systems, and this is much less straightforward. Sparse versions of some of the decompositions that we met before are needed, but naive implementations using sparse matrices flounder on the problem of infill (or fill-in). You can see the problem in the following dense calculation

system.time({ XX <- t(X)%*%X; R <- chol(XX) })

   user  system elapsed 
  5.175   0.114   5.295

dim(XX)

[1] 400 400

sum(XX == 0)/prod(dim(XX))

[1] 0.97935

image(as(XX,"Matrix"))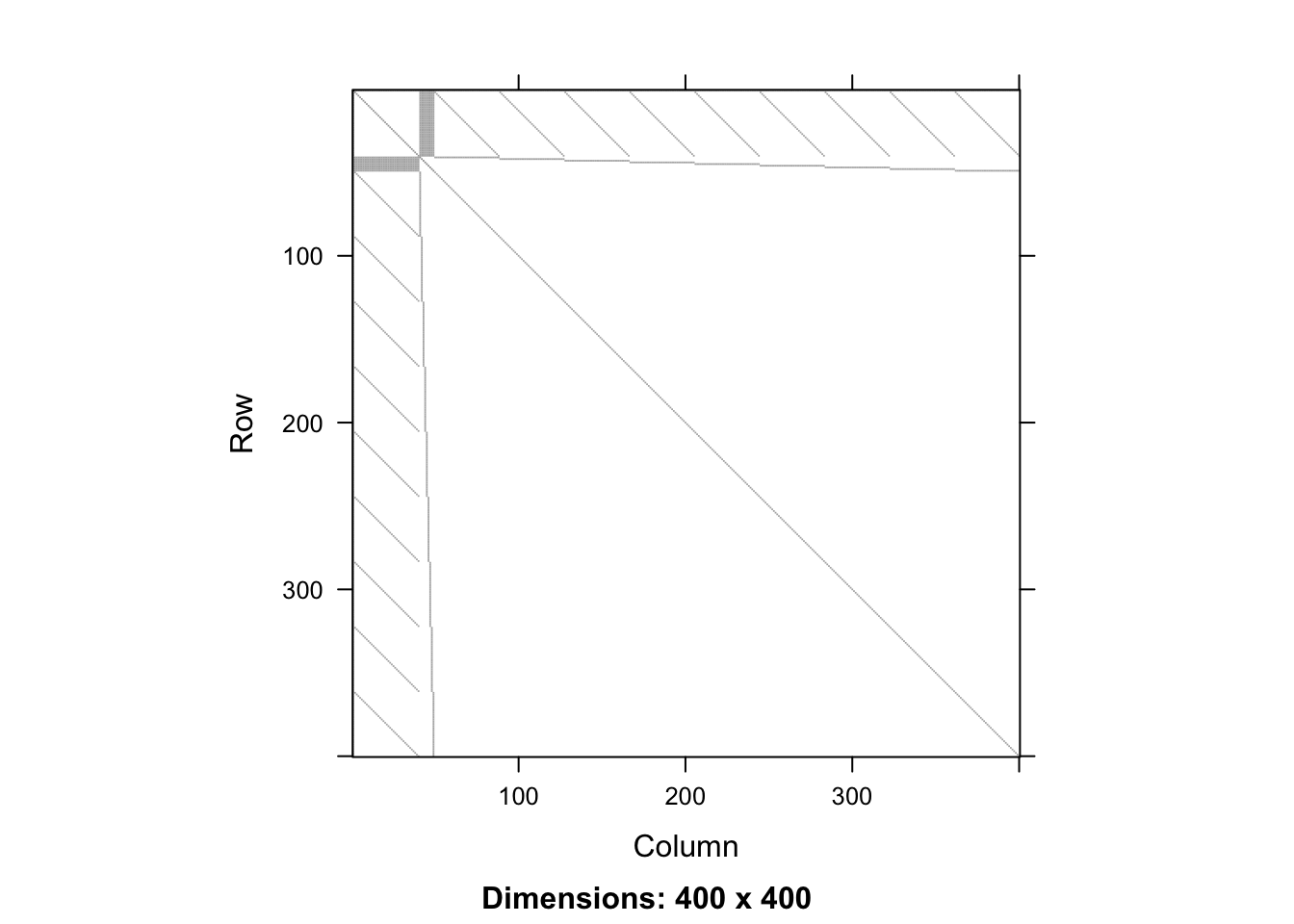

range(t(R)%*%R-XX)

[1] -1.818989e-12  1.455192e-11

sum(R != 0) ## the upper triangle is dense (not good)

[1] 80200

image(as(R,"Matrix"))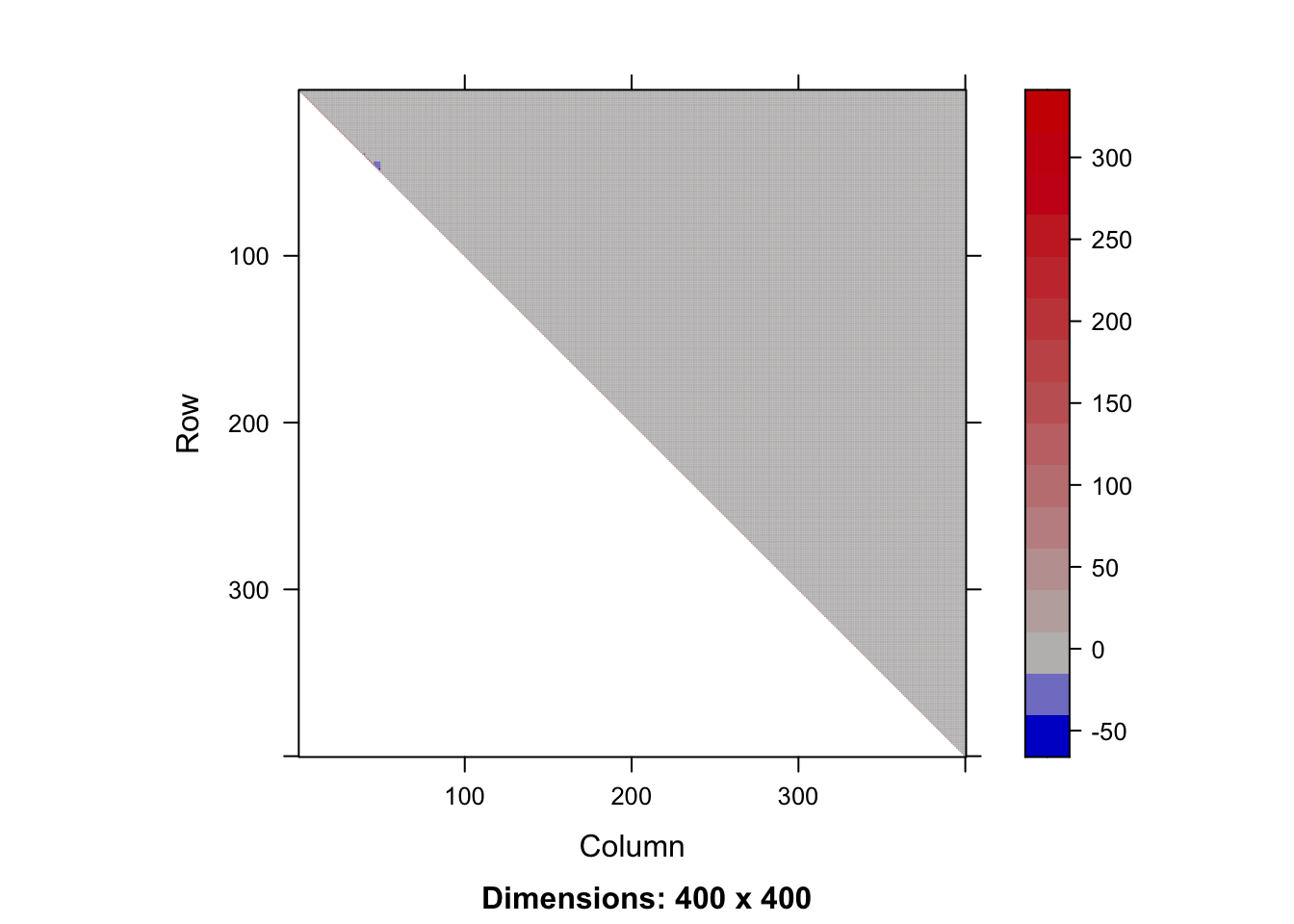

R[1:5, 1:5] ## top left corner, for example

            (Intercept)        a2        a3        a4        a5
(Intercept)    316.2278  7.807664  7.968940  7.791852  8.139703
a2               0.0000 49.071788 -1.267914 -1.239738 -1.295083
a3               0.0000  0.000000 49.546830 -1.284940 -1.342303
a4               0.0000  0.000000  0.000000 48.990805 -1.362576
a5               0.0000  0.000000  0.000000  0.000000 50.024090

Although \({\bf X}^{\sf T}{\bf X}\) is 98% zeroes, the upper triangle of its Cholesky factor is 0% zeroes, when computed in the usual way. i.e. we have lost all sparsity. Fortunately, it is possible to re-arrange the rows and columns of \({\bf X}^{\sf T}{\bf X}\) (or any other matrix for which we need a sparse Cholesky factor), in a way that reduces infill in the Cholesky factor. This pivoting means that we get a re-ordered version of the solution of the system of interest: a minor inconvenience. Unfortunately, finding the optimal pivoting in terms of infill reduction is NP hard, but there are never the less practical computational pivoting strategies that work well in practice. These rely on some rather ingenious graph theory based symbolic analysis of the matrix to be factorised, which is applied before anything numerical is computed. See Davis (2006). Here’s what happens when a sparse Cholesky factorisation, with infill reducing pivoting, is used on \({\bf X}^{\sf T}{\bf X}\)

  system.time({
    XXs <- t(Xs)%*%Xs
    chX <- Cholesky(XXs,perm=TRUE) ## pivoting reduces infill
    Rs <- t(expand1(chX,"L")) ## extract actual factor
  })

   user  system elapsed 
  0.007   0.000   0.010

  piv <- chX@perm+1
  range(t(Rs)%*%Rs-XXs[piv,piv]) ## factorization works!

[1] -5.684342e-14  4.547474e-13

  sum(Rs!=0) ## the upper triangle is sparse (much better)

[1] 1501

  image(Rs)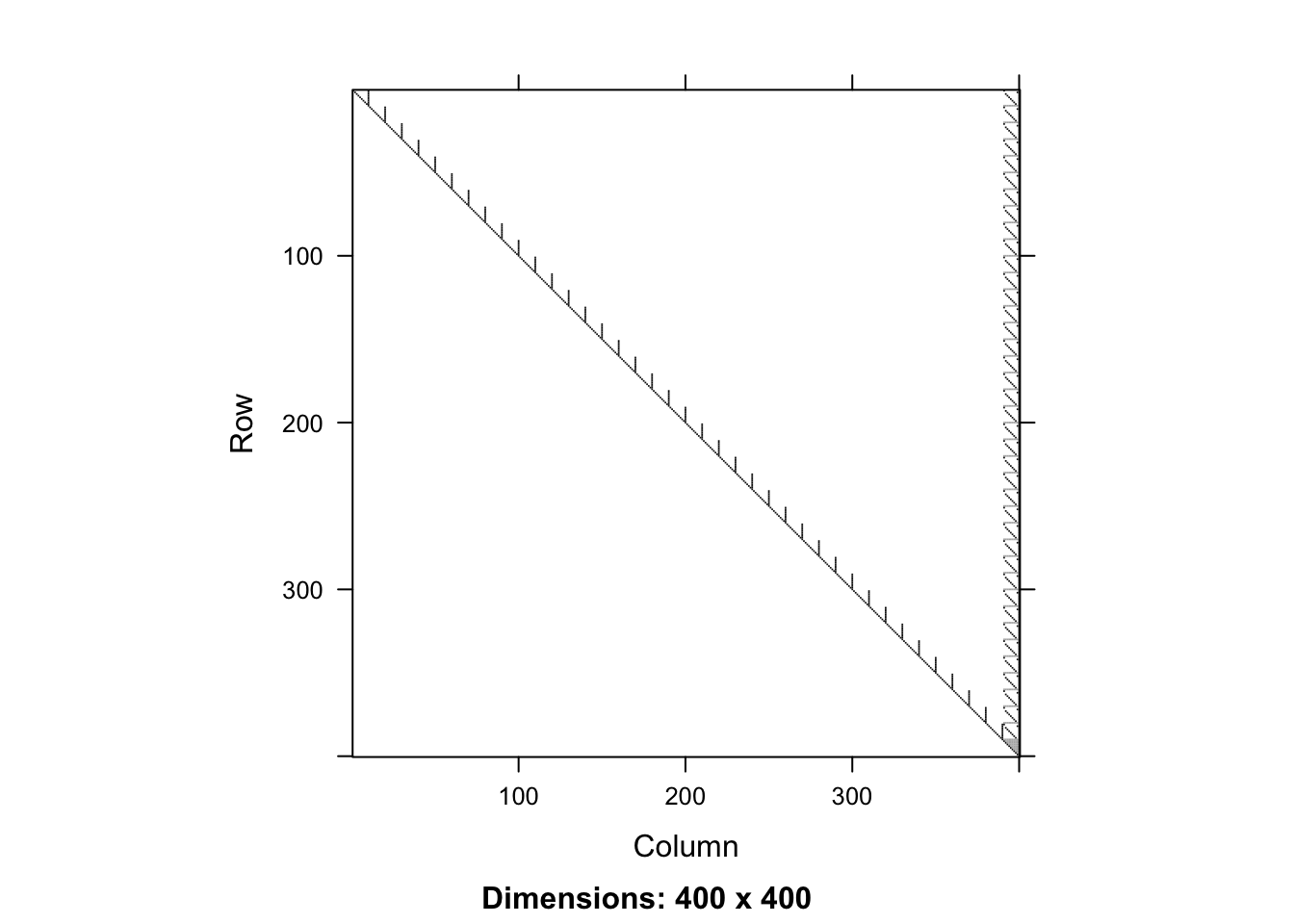

  Rs[1:5,1:5] ## top left corner, for example

5 x 5 sparse Matrix of class "dtCMatrix"
                                               
[1,] 15.6205  .        .        .       .      
[2,]  .      15.68439  .        .       .      
[3,]  .       .       16.24808  .       .      
[4,]  .       .        .       14.8324  .      
[5,]  .       .        .        .      15.45962

with sparsity maintained in the factor, sparse backward or forward substitution is also very efficient.

Note that while the sparse Cholesky routines in the Matrix package are state-of-the-art, the QR routines are not, and carry heavy memory overheads associated with computation of \({\bf Q}\). You’ll probably need to look for sparse multi-frontal QR routines if you need sparse QR.

3 Hashing: another example

Suppose that you want to store data, which is to be accessed using arbitrary keys. For example, you want to store data on a large number of people, using their names (as a text string) as the key for finding the record in memory. i.e., data about someone is read in from somewhere, and is stored at a location in computer memory, depending on what their name string is. Later you want to retrieve this information using their name string. How can you actually do this?

You could store some sort of directory of names, which would be searched through to find the location of the data. But such a search is always going to take some time, which will increase with the number of people’s data that is stored. Can we do better? With hashing the answer is yes. The pivotal idea is to create a function which will turn an arbitrary key into an index which is either unique or shared with only a few other keys, and has a modest predefined range. This index gives a location in a (hash) table which in turn stores the location of the actual data (plus some information for resolving `clashes’). So given a key, we use the (hash) function to get its index, and its index to look up the data location, with no, or very little searching. The main problem is how to create a hash function.

An elegant general strategy is to use the ideas of pseudorandom number generation to turn keys into random integers. For example, if the key were some 64bit quantity, we could use it to seed the Xorshift random number generator given earlier, and run this forward for a few steps. More generally we would need an approach that successively incorporated all the bits in a key into the `random number’ generation process (see e.g. section 7.6 of Press et al., 2007, for example code). So, the hash function should return numbers that appear random, which will mean that they tend to be nicely spread out, irrespective of what the keys are like. Of course, despite this, the function always returns the same number for a given key.

It remains to turn the number returned by the hash function, \(h\), into an index, \(i_h\) , somewhere between 0 and the length, \(n_h\), of the hash table minus 1. \(i_h = h~ {\rm mod}~ n_h\) is the usual approach. At position \(i_h\) in the hash table we might store the small number of actual keys (or possibly just their \(h\) values) sharing the \(i_h\) value, and the actual location in memory of the corresponding data.

The really neat thing here is that the randomness of the \(h\)’s means that whatever the keys look like, you usually end up with a fairly uniform distribution of \(i_h\)’s, and only a small number of keys sharing each slot in the hash table. It is this that makes data retrieval so efficient, relative to searching a directory of keys.

Note that R environments are themselves methods for associating values with lookup keys, and in fact, R environments can use hash tables: see ?new.env.

ht <- new.env(hash=TRUE)
ht[["foo"]] = "bar"
ht[["baz"]] = 1:10
ht[["foo"]]

[1] "bar"

ht$baz

 [1]  1  2  3  4  5  6  7  8  9 10

If that doesn’t sound like it has any application in statistics, consider the construction of triangulations in spatial statistics (a triangulation being a way of joining a set of points up with triangles, in such a way that the whole convex hull of the points is covered in triangles). Efficient construction of triangulations is tricky, and several efficient algorithms work by incrementally adding triangles. You usually know at least one neighbour of each triangle at its creation, but you actually need to know all its neighbours in the existing set. The task of finding those neighbours would be prohibitive if you had to search each existing triangle for edges shared with the new triangle. Instead one can maintain a hash table for unpaired triangle edges, where the hash key is based on the end co-ordinates of each edge. This allows any newly created edge to be paired with any existing edge in little more than the length of time it takes to create the hash key.

4 Further reading

Gentle, J.E. (2003) Random Number Generation and Monte Carlo Methods (2nd ed), Springer, Chapters 1 and 2 provides up to date summaries both of uniform generators, and of generator testing. Chapter 3 covers Quasi Monte Carlo, and the remaining chapters cover simulation from other distributions + software.
Matsumoto, M. and Nishimura, T. (1998) Mersenne Twister: A 623-dimensionally equidistributed uniform pseudo-random number generator, ACM Transactions on Modeling and Computer Simulation, 8, 3-30. This gives details and code for the Mersenne Twister.
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html gives the Mersenne Twister source code.
Marsaglia, G. (2003) Xorshift RNGs, Journal of Statistical Software, 8(14):1-6.
DIEHARD is George Marsaglia’s Diehard battery of tests for random number generators
Press, W.H., S.A. Teukolsky, W.T. Vetterling and B.P Flannery (2007) Numerical Recipes (3rd ed.) Cambridge. Chapter 7, on random numbers is good and reasonably up to date, but in this case you do need the third edition, rather than the second (and certainly not the first).
Ripley (1987, re-issued 2006) Stochastic Simulation, Wiley. Chapter’s 2 and 3 are where to go to really get to grips with the issues surrounding random number generation. The illustrations alone are an eye opener. You probably would not want to use any of the actual generators discussed and the remarks about mixed generators now look dated, but the given principles for choosing generators remain sound (albeit with some updating of what counts as simple, and the integers involved). See chapter 3 and 4 for simulating from other distributions, given uniform deviates.
Gamerman, D. and H.F. Lopes (2006) Markov Chain Monte Carlo: Stochastic simulation for Bayesian inference, CRC. Chapter 1 has a nice compact introduction to simulation, given i.i.d. \(U(0,1)\) deviates.
Devroye, L., (2003) Non-Uniform Random Variate Generation, Springer. This is a classic reference. Now out of print.
Steele Jr, Guy L., Doug Lea, and Christine H. Flood. “Fast splittable pseudorandom number generators.” ACM SIGPLAN Notices 49.10 (2014): 453-472. In the context of parallel computing, sequential random number generators are very problematic. Splittable generators turn out to be very useful in this context.
For a good introduction to the sparse methods underlying Martin Maechler and Douglas Bates’ R package Matrix, see Davis, T. A. (2006) Direct Methods for Sparse Linear Systems, SIAM.
Tim Davis’s home page is worth a look for more recent sparse matrix developments.
If you think hashing is clever, take a look at the rest of Cormen, T., C.E. Leiserson, R.L. Rivest and C. Stein (2001) Introduction to Algorithms (2nd ed.) MIT.
Once again, Press, W.H., S.A. Teukolsky, W.T. Vetterling and B.P Flannery (2007) Numerical Recipes (3rd ed.) provides a readable introduction to a much wider range of topics in scientific computing than has been covered here.