Optimization
Many problems in statistics can be characterised as solving
\[ \underset{{\bf \theta}}{\rm min} f(\boldsymbol{\theta}) \tag{1}\] where \(f\) is a real scalar valued function of vector \(\boldsymbol{\theta}\), usually known as the objective function. For example: \(f\) might be the negative log-likelihood of the parameters \(\boldsymbol{\theta}\) of a statistical model, the maximum likelihood estimates of which are required; in a Bayesian setting \(f\) might be a (negative) posterior distribution for \(\boldsymbol{\theta}\), the posterior modes of which are required; \(f\) might be a dissimilarity measure for the alignment of two DNA sequences, where the alignment is characterised by a parameter vector \(\boldsymbol{\theta}\); \(f\) might be total distance travelled, and \(\boldsymbol{\theta}\) a vector giving the order in which a delivery van should visit a set of drop off points. Note that maximising \(f\) is equivalent to minimising \(-f\) so we are not losing anything by concentrating on minimisation here. In the optimization literature, the convention is to minimise an objective, with the idea being that the objective is some kind of cost or penalty to be minimised. Indeed, the objective function is sometimes referred to as the cost function.
Let \(\Theta\) denote the set of all possible \(\boldsymbol{\theta}\) values. Before discussing specific methods, note that in practice we will only be able to solve Equation 1 if one of two properties holds:
- It is practical to evaluate \(f(\boldsymbol{\theta})\) for all elements of \(\Theta\).
- It is possible to put some structure onto \(\Theta\), giving a notion of distance between any two elements of \(\Theta\), such that closeness in \(\Theta\) implies closeness in \(f\) value.
In complex situations, requiring complicated stochastic approaches, it is easy to lose sight of point 2 (although if it isn’t met we may still be able to find ways of locating \(\theta\) values that reduce \(f\)).
Optimization problems vary enormously in difficulty. In the matrix section we saw algorithms with operation counts which might be proportional to as much as \(n^3\). There are optimization problems whose operations count is larger than \(O(n^k)\) for any \(k\): in computer science terms there is no polynomial time algorithm for solving them. Most of these really difficult problems are discrete optimization problems, in that \(\boldsymbol{\theta}\) takes only discrete values, rather than consisting of unconstrained real numbers. One such problem is the famous Travelling salesman problem, which is concerned with finding the shortest route between a set of fixed points, each to be visited only once. Note however, that simply having a way of improving approximate solutions to such problems is usually of considerable practical use, even if exact solution is very taxing.
Continuous optimization problems are generally more straightforward than discrete problems, and we will concentrate on such problems here. In part this is because of the centrality of optimization methods in practical likelihood maximisation.
Computer scientists have an interesting classification of the ‘difficulty’ of problems that one might solve by computer. If \(n\) is the problem ‘size’ then the easiest problems can be solved in polynomial time: they require \(O(n^k)\) operations where \(k\) is finite. These problems are in the P-class. Then there are problems for which a proposed solution can be checked in polynomial time, the NP class. NP-complete problems are problems in NP which are at least as hard as all other problems in NP in a defined sense. NP hard problems are at least as hard as all problems in NP, but are not in NP: so you can’t even check the answer to an NP hard problem in polynomial time. No one knows if P and NP are the same, but if any NP-complete problem turned out to be in P, then they would be.
1 Local versus global optimization
Minimisation methods generally operate by seeking a local minimum of \(f\). That is they seek a point, \(\boldsymbol{\theta}^*\), such that \(f(\boldsymbol{\theta}^*+\boldsymbol{\Delta}) \ge f(\boldsymbol{\theta}^*)\), for any sufficiently small perturbation \(\boldsymbol{\Delta}\). Unless \(f\) is a strictly convex function, it is not possible to guarantee that such a \(\boldsymbol{\theta}^*\) is a global minimum. That is, it is not possible to guarantee that \(f(\boldsymbol{\theta}^*+\boldsymbol{\Delta}) \ge f(\boldsymbol{\theta}^*)\) for any arbitrary \(\boldsymbol{\Delta}\).
2 Optimization methods are myopic
Before going further it is worth stressing another feature of most widely-used optimization methods: they are generally very short-sighted. At any stage of operation all that optimization methods ‘know’ about a function are a few properties of the function at the current best \(\boldsymbol{\theta}\), (and, much less usefully, those same properties at previous best points). It is on the basis of such information that a method tries to find an improved best \(\boldsymbol{\theta}\). The methods have no ‘overview’ of the function being optimized.
3 Look at your objective first
Before attempting to optimize a function with respect to some parameters, it is a good idea to produce plots in order to get a feel for the function’s behaviour. Of course if you could simply plot the function over the whole of \(\Theta\) it is unlikely that you would need to worry about numerical optimization, but generally this is not possible, and the best that can be achieved is to look at some slices of \(f\), across one or two parameters (as done below).
To fix ideas, consider the apparently innocuous example of fitting a simple dynamic model to a single time series by least squares/maximum likelihood. The dynamic model is the so-called logistic map, that is \[ n_{t+1} = rn_t (1-n_t/K),~~~~t=0,1,2,\ldots \] where \(n_t\) is the population at time \(t\), while \(r\) and \(K\) are parameters representing, respectively, the growth rate and the carrying capacity, the latter being the maximum population size the environment can sustain. We will assume that the initial population, \(n_0\), is known. Further, suppose that we have noisy observations \(y_t = n_t + \epsilon_t\) where \(\epsilon_t \underset{\rm i.i.d.}{\sim} N(0,\sigma^2)\).
Estimation of \(r\) and \(K\) by least squares (equivalent to maximum likelihood, in this case) requires minimisation of \[ f(r,K) = \sum_{t=1}^T ( y_t - n_t )^2 \] w.r.t. \(r\) and \(K\), where \(T\) is the number of observations and \(n_t\) is implicitly a function of \(r\) and \(K\). We should try to get a feel for the behaviour of \(f\). To see how this can work consider some simulated data examples. In each case I used \(T = 50\), \(n_0 = 20\), \(K=50\) and \(\sigma=1\) for the simulations, but I have varied \(r\) between the cases.
In the first instance data were simulated with \(r=2\). If we now pretend that we need to estimate \(r\) and \(K\) from such data, then we might look at some slices of \(f\) across \(r\) (keeping \(K\) fixed at 50). This figure shows the raw data and an \(r\)-slice.
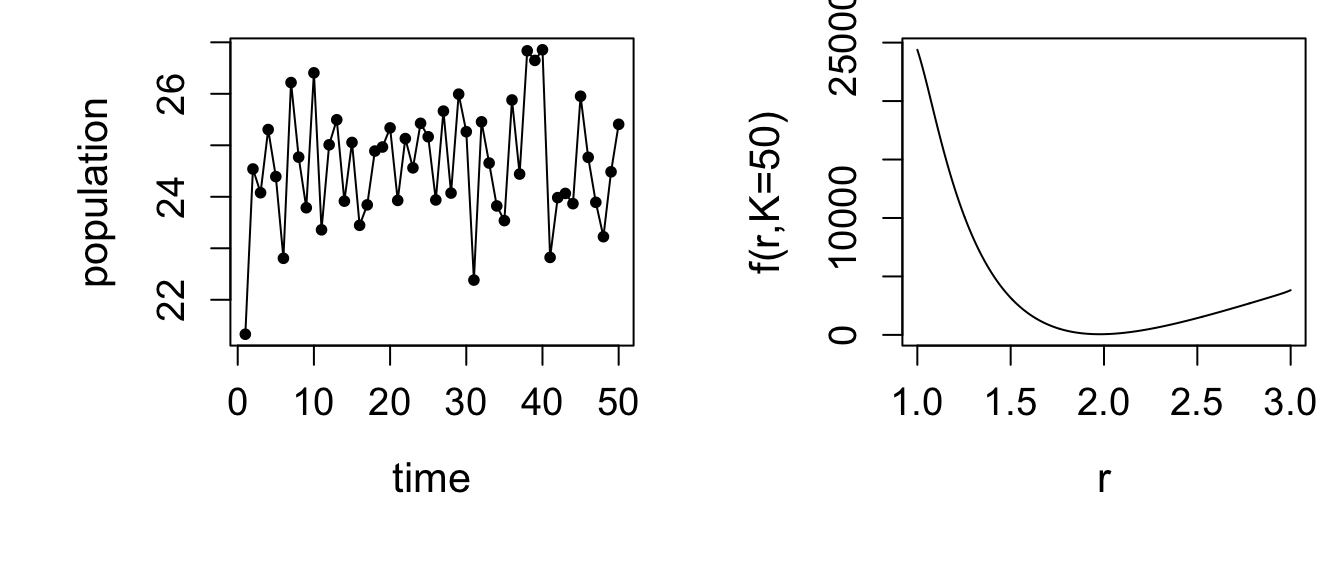
Similar \(r\)-slices (not shown) with other \(K\) values look equally innocuous (i.e., smooth and with unique minimum), and slices across \(K\) (not shown) also look ok (with \(r\) fixed to around 2). So in this case \(f\) appears to be a nice smooth function of \(r\) and \(K\), and any decent optimization method ought to be able to find the optimum.
In the second example data were simulated with \(r=3.2\). Again pretend that we only have the data and need to estimate \(r\) and \(K\) from it. Examination of the left hand plot below, together with some knowledge of the model’s dynamic behaviour (see this), indicates that \(r\) is probably in the 3 to 4 range.
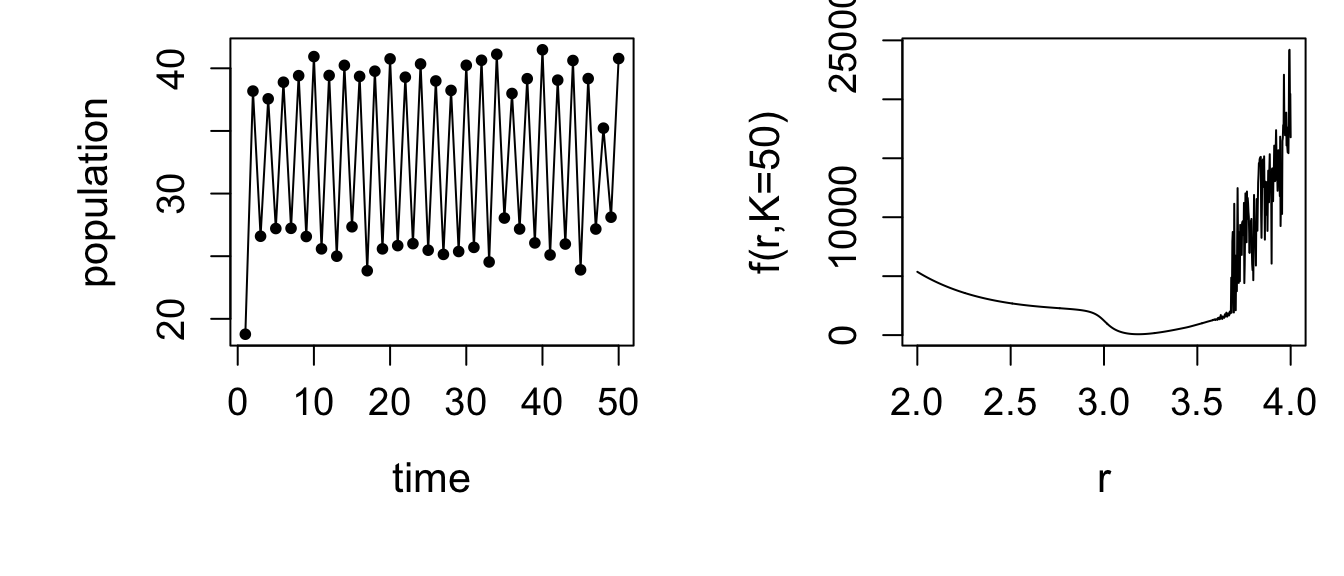
Notice that \(f\) still seems to behave smoothly in the vicinity of its minimum, which is around 3.2, but that something bizarre starts to happen above 3.6. Apparently we could be reasonably confident of locating the function’s minimum if we start out below or reasonably close to 3.2, but if we stray into the territory above 3.6 then there are so many local minima that locating the desired global minimum would be very difficult.
Finally data were simulated with \(r=3.8\).
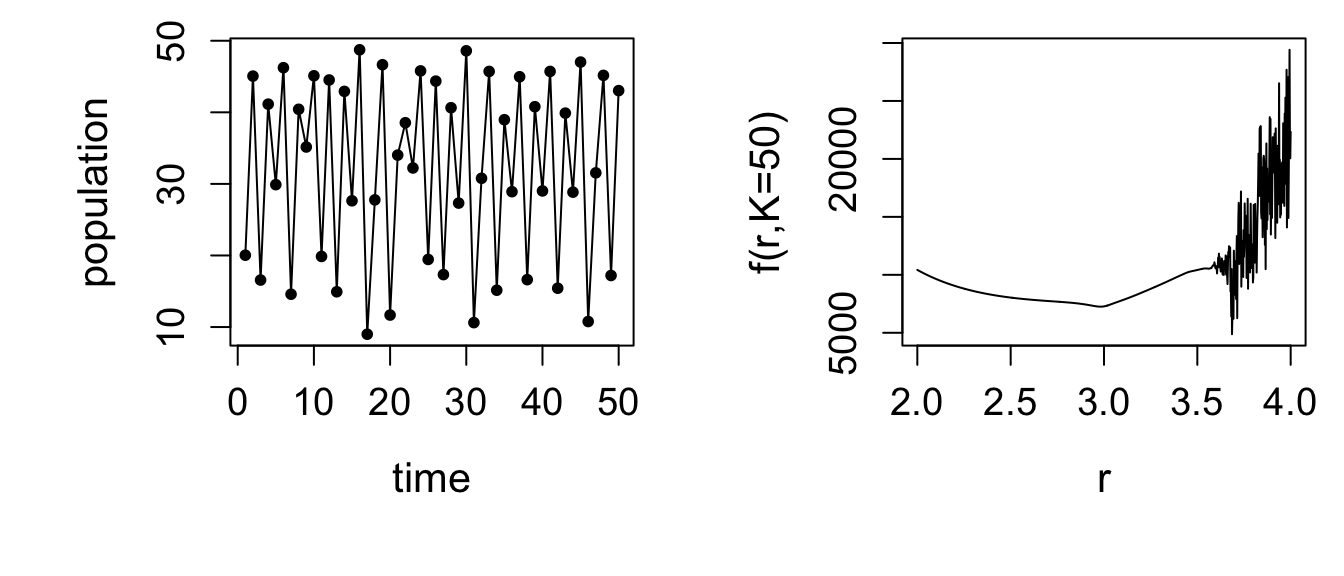
Now the objective has a minimum somewhere around 3.7, but it is surrounded by other local minima, so that locating the actual minima would be a rather taxing problem. In addition it is now unclear how we would go about quantifying uncertainty about the ‘optimal’ \(\boldsymbol{\theta}\). For example, it will certainly be of no use appealing to the asymptotic normality of the maximum likelihood estimator in this case.
So, in each of these examples, simple slices through the objective function have provided useful information. In the first case everything seemed OK. In the second we would need to be careful with the optimization, and careful to examine how sensible the optimum appeared to be. In the third case we would need to think very carefully about the purpose of the optimization, and about whether a re-formulation of the basic problem might be needed.
Notice how the behaviour of the objective was highly parameter dependent here, something that emphasises the need to understand models quite well before trying to fit them. In this case the dynamic model, although very simple, can show a wide range of complicated behaviour, including chaos. In fact, for this simple example, it is possible to produce a plot of the fitting objective over pretty much the whole plausible parameter space. Here is an example when data were simulated with \(r=3.2\)
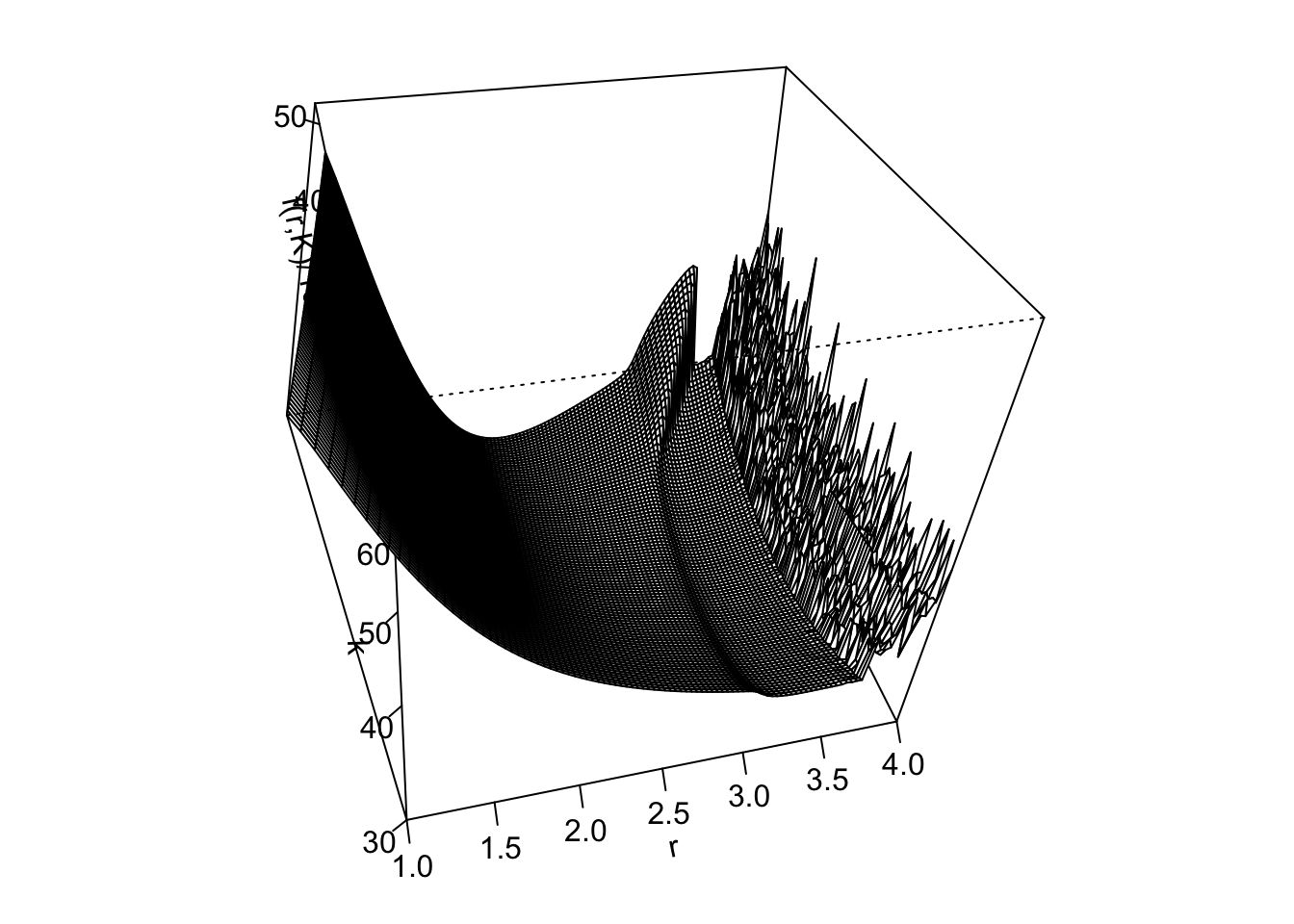
3.1 Objective function slices are a partial view
Clearly plotting some slices through your objective function is a good idea, but they can only give a limited and partial view when the \(\boldsymbol{\theta}\) is multidimensional. Consider this \(x\)-slice through a function, \(f(x,y)\)
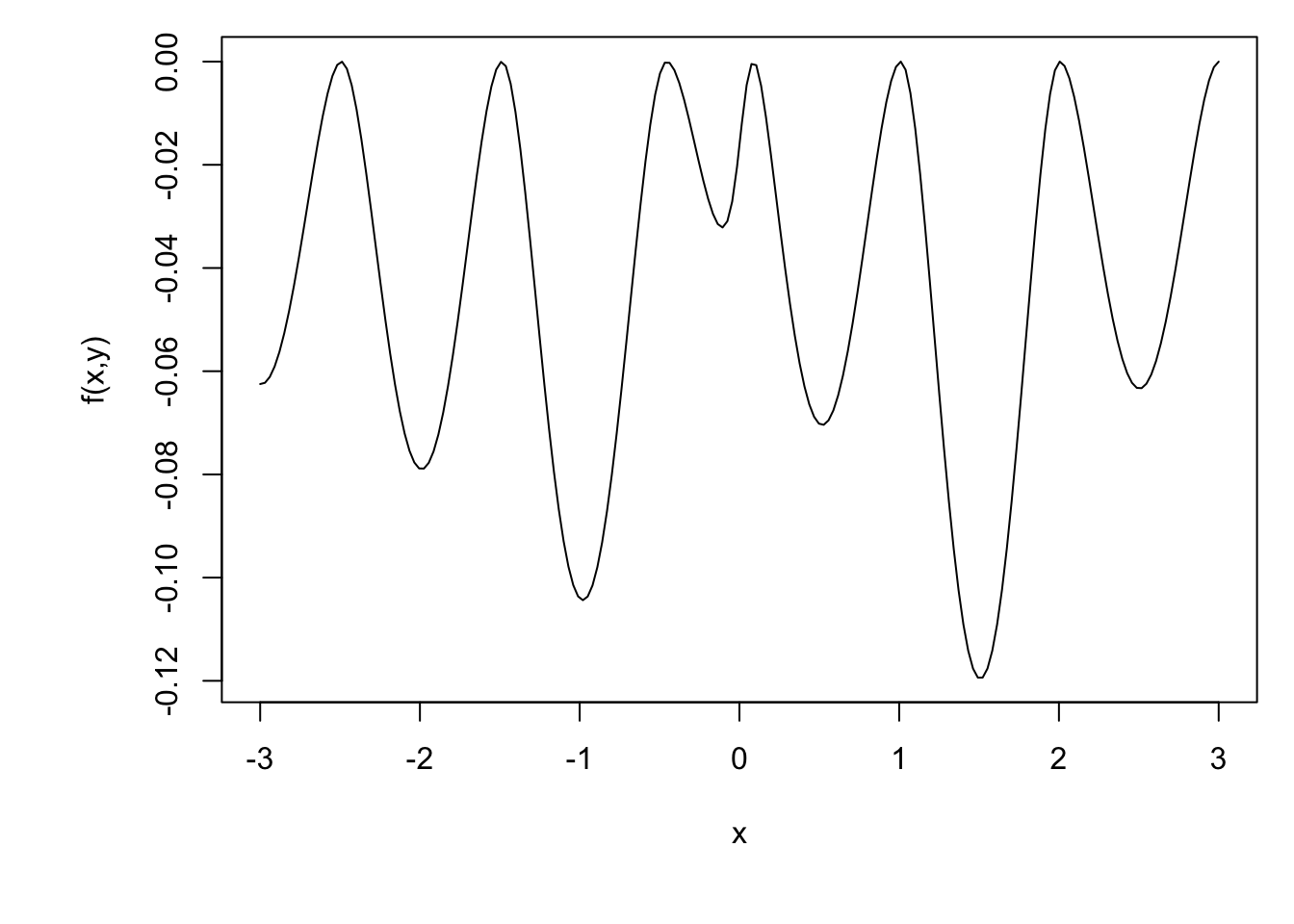
From the slice is appears that the function has many local minima, and optimization will be difficult. But, actually, the function is this
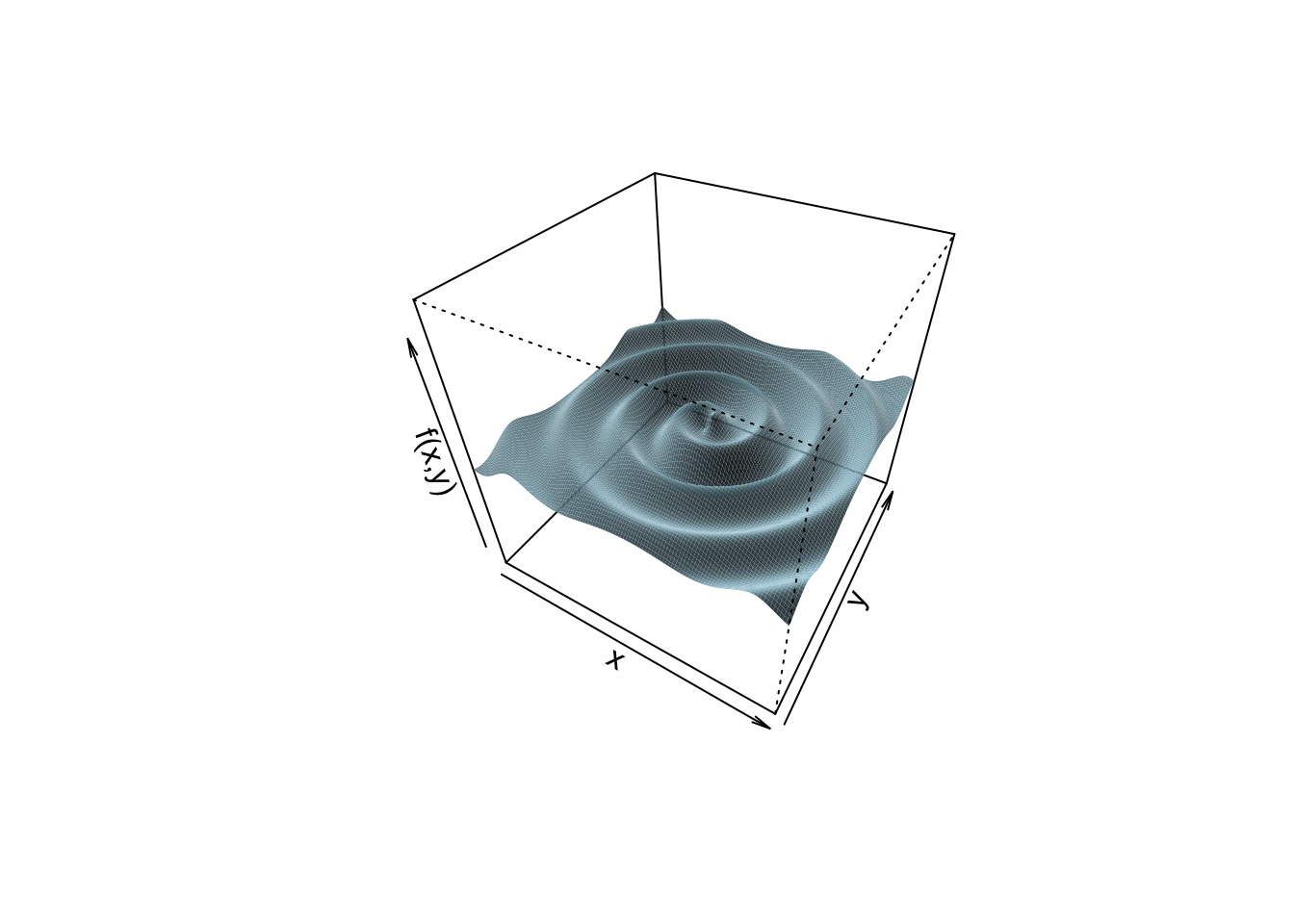
It has one local minimum, its global minimum. Head downhill from any point \(x,y\) and you will eventually reach the minimum. So this, somewhat artificial, example shows that looking at one-dimensional slices of an objective function might give you the impression that an optimisation problem is harder than it really is.
The opposite problem can also occur. Here are \(x\) and \(y\) slices through a second function \(g(x,y)\).
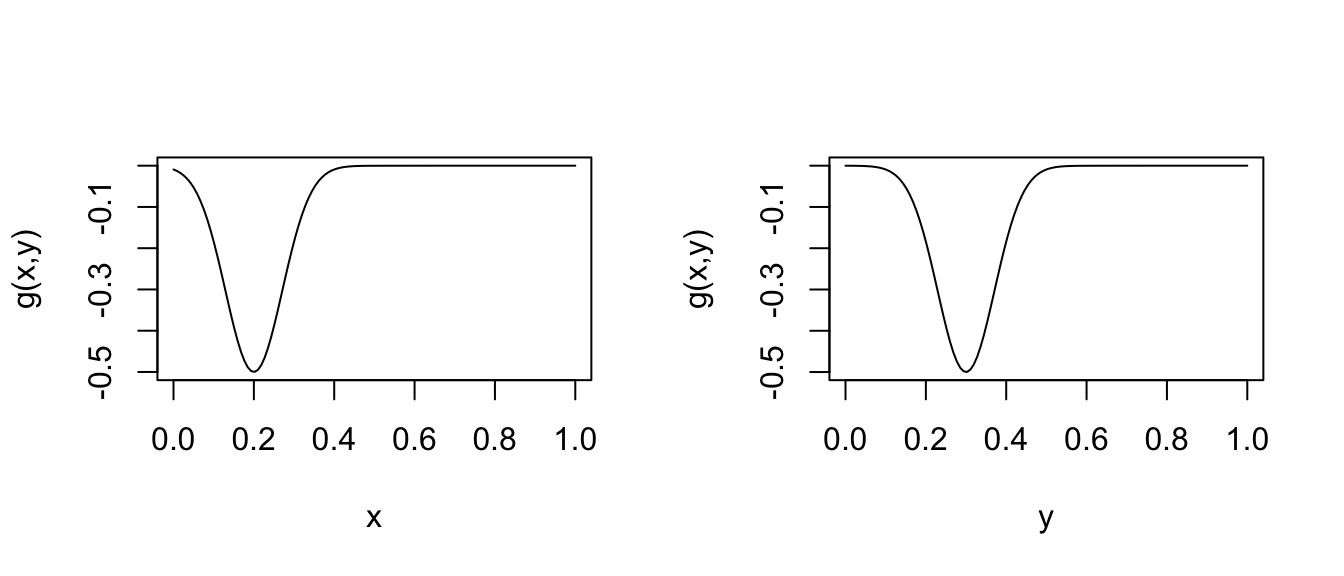
The slices show no problem, so you would be tempted to conclude that \(g\) is a well behaved and has a unique minimum. The problem is that \(g\) looks like this
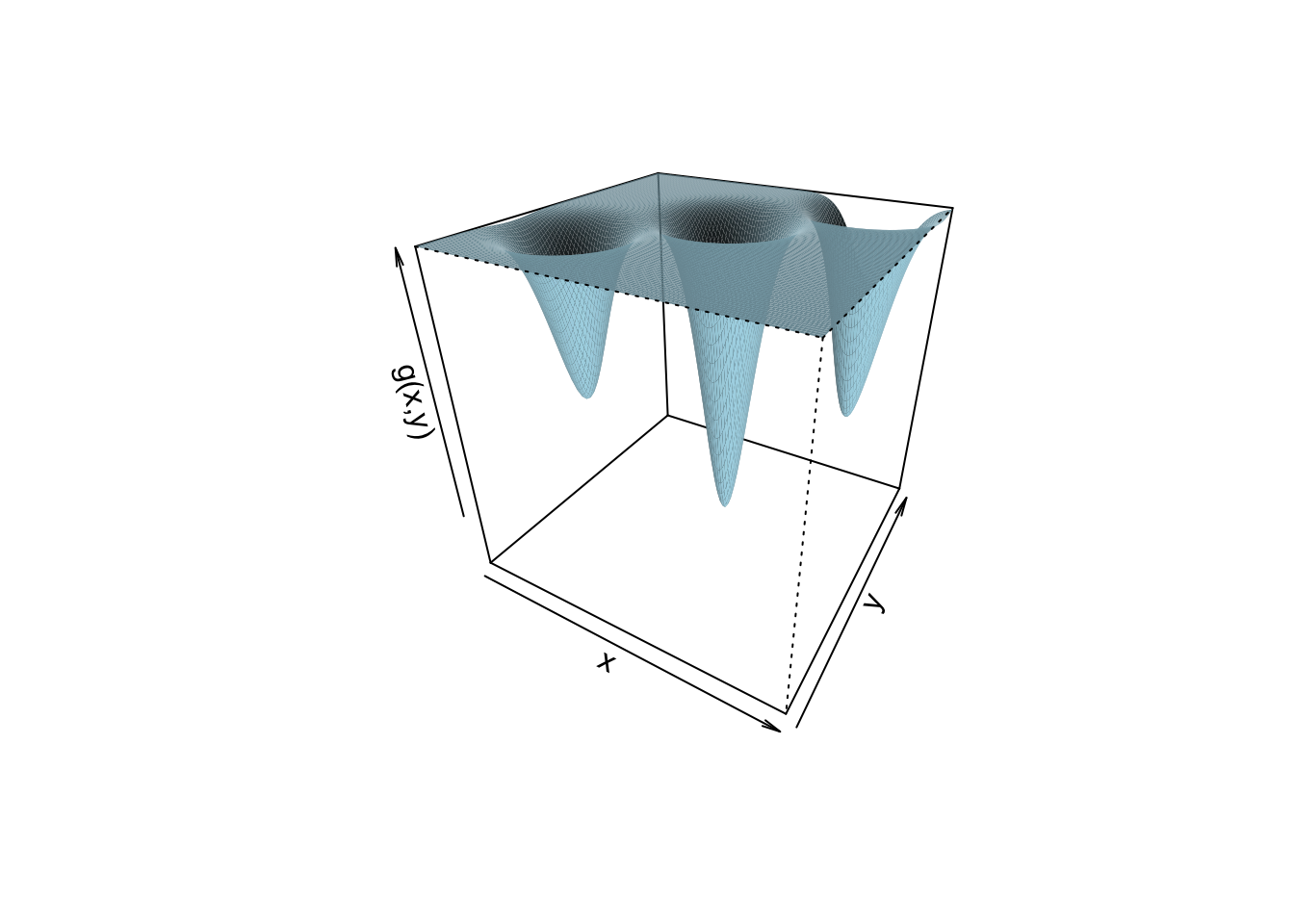
That is, it has three local minima, and only one of them is the global minimum. Whether any of the optimisation methods described below reaches the global minimum, or gets stuck in one of the local minima, depends on the chosen initial value. In conclusion, it is generally a good idea to plot slices through your objective function before optimization, and to plot slices passing through the apparent optimum after optimization, but bear in mind that slices only give partial views.
4 Some optimization methods
Optimization methods start from some initial guess of the optimum, \(\boldsymbol{\theta}^{[0]}\). Starting from iteration \(k=0\), most methods then iterate the following steps:
evaluate \(f(\boldsymbol{\theta}^{[k]})\), and possibly the first and second derivatives of \(f\) w.r.t. the elements of \(\boldsymbol{\theta}\), at \(\boldsymbol{\theta}^{[k]}\).
Use the information from step 1 (and possibly previous executions of step 1) to either
- find a search direction, \(\boldsymbol{\Delta}\), such that for some \(\alpha\), \(f({\boldsymbol{\theta}^{[k]}} + \alpha \boldsymbol{\Delta})\) will provide sufficient decrease relative to \(f({\boldsymbol{\theta}^{[k]}})\). Search for such an \(\alpha\) and set \({\boldsymbol{\theta}^{[k+1]}} = {\boldsymbol{\theta}^{[k]}} + \alpha \boldsymbol{\Delta}\).
Or
- construct a local model of \(f\), and find the \(\boldsymbol{\theta}\) minimising this model within a defined region around \({\boldsymbol{\theta}^{[k]}}\). If this value of \(\boldsymbol{\theta}\) leads to sufficient decrease in \(f\) itself, accept it as \(\boldsymbol{\theta}^{[k+1]}\), otherwise shrink the search region until it does.
Test whether a minimum has yet been reached. If it has, terminate, otherwise increment \(k\) and return to step 1.
Methods employing approach (a) at step 2 are known as search direction methods, while those employing approach (b) are trust region methods. In practice the difference between (a) and (b) may be rather small: the search direction is often based on a local model of the function. Here we will examine some search direction methods.
4.1 Taylor’s Theorem (and conditions for an optimum)
We need only a limited version of Taylor’s theorem. Suppose that \(f\) is a twice continuously differentiable function of \(\boldsymbol{\theta}\) and that \(\boldsymbol{\Delta}\) is of the same dimension as \(\boldsymbol{\theta}\). Then \[ f(\boldsymbol{\theta} + \boldsymbol{\Delta}) = f(\boldsymbol{\theta}) + \nabla f(\boldsymbol{\theta}) ^{\sf T}\boldsymbol{\Delta} + \frac{1}{2} \boldsymbol{\Delta} ^{\sf T}\nabla^2 f(\boldsymbol{\theta}) \boldsymbol{\Delta} + R^2_{\boldsymbol{\theta}}(\boldsymbol{\Delta}), \tag{2}\] where \[ \nabla f(\boldsymbol{\theta}) = \left ( \begin{array}{c} \frac{\partial f}{\partial \theta_1} \\ \frac{\partial f}{\partial \theta_2} \\ . \\ . \end{array}\right ){\rm ~~ and ~~} \nabla^2 f(\boldsymbol{\theta}) = \left ( \begin{array}{cccc} \frac{\partial ^2f}{\partial \theta_1^2} & \frac{\partial^2 f}{\partial \theta_1 \partial \theta_2} & . & . \\ \frac{\partial^2 f}{\partial \theta_2 \partial \theta_1} & \frac{\partial ^2 f}{\partial \theta_2^2} & . & . \\ . & . & . & . \\ . & . & . & . \end{array}\right ), \] and \(R^2_{\boldsymbol{\theta}}(\boldsymbol{\Delta})\) is the remainder of the expansion, the superscript \(2\) indicating that the remainder includes derivatives of order higher than two. The remainder goes to zero as \(\boldsymbol{\Delta} \rightarrow \bf 0\), which means that, if we drop the remainder from the r.h.s. of Equation 2, we can use the remaining terms on the r.h.s as an approximation to \(f\), in the vicinity of \(\boldsymbol \theta\). From Taylor’s theorem it is straightforward to establish (if unsure, try to do it) that the conditions for \(f(\boldsymbol{\theta}^*)\) to be a local minimum of \(f\) are that \(\nabla f(\boldsymbol{\theta}^*) = {\bf 0}\) and \(\nabla^2 f(\boldsymbol{\theta}^*)\) is positive semi-definite.
In optimisation problems, we typically work with the approximate versions of the above result, where the remainder is discarded. When working with a quadratic (second-order) approximation to \(f\), this implies that \(R^2_{\boldsymbol{\theta}}(\boldsymbol{\Delta})\) is discarded from Equation 2. When working with a linear (first-order) approximation to \(f\), this involves discarding \(R^1_{\boldsymbol{\theta}}(\boldsymbol{\Delta})\), which now includes derivatives of order higher than one.
4.2 Steepest descent (AKA gradient descent)
Given some parameter vector \(\boldsymbol{\theta}^{[k]}\), it might seem reasonable to simply ask which direction would lead to the most rapid decrease in \(f\) for a sufficiently small step, and to use this as the search direction. If \(\boldsymbol{\Delta}\) is small enough then Taylor’s theorem implies that \[ f(\boldsymbol{\theta}^{[k]} + \boldsymbol{\Delta}) \simeq f(\boldsymbol{\theta}^{[k]}) + \nabla f(\boldsymbol{\theta}^{[k]}) ^{\sf T}\boldsymbol{\Delta}. \] For \(\boldsymbol{\Delta}\) of fixed length \(0 < \alpha \ll 1\) the greatest decrease will be achieved by minimising the inner product \(\nabla f(\boldsymbol{\theta}^{[k]}) ^{\sf T}\boldsymbol{\Delta}\), which is achieved by making \(\boldsymbol{\Delta}\) parallel to \(-\nabla f(\boldsymbol{\theta}^{[k]})\), i.e. by choosing \[ \boldsymbol{\Delta} = -\alpha \frac{\nabla f(\boldsymbol{\theta}^{[k]})}{||\nabla f(\boldsymbol{\theta}^{[k]})||}, \] where \(||\cdot||\) indicates the Euclidean norm. To see this, consider a new proposed value of the form \(\boldsymbol{\theta}^{[k]}+\alpha {\bf u}\), where \(\bf u\) is a unit vector. Then, by plugging back into our linear approximation, we have \[\begin{align*} f(\boldsymbol{\theta}^{[k]}+\alpha \boldsymbol{\Delta}) &\simeq f(\boldsymbol{\theta}^{[k]}) + \alpha\nabla f(\boldsymbol{\theta})^{\sf T}{\bf u} \\ & = f(\boldsymbol{\theta}^{[k]}) + \alpha \| \nabla f(\boldsymbol{\theta}^{[k]}) \| \text{cos}(\phi), \end{align*}\] where \(\phi\) is the angle between \(\nabla f(\boldsymbol{\theta}^{[k]})\) and \(\bf u\). Clearly, the last expression is minimised when \(\phi = \pi\), that is when we are moving in the direction of \(-\nabla f(\boldsymbol{\theta}^{[k]})\).
Even though the first-order Taylor expansion on which steepest descent relies becomes increasingly accurate as \(\alpha \rightarrow 0\), we clearly do not what to make infinitesimal steps along \(\nabla f(\boldsymbol{\theta}^{[k]})\), otherwise converging to the minimum will take forever. Instead, given a search direction \(\boldsymbol{\Delta} = -\nabla f(\boldsymbol{\theta}^{[k]})\), we need a method for choosing how far to move from \(\boldsymbol{\theta}^{[k]}\) along this direction. To decide the step size, we have to consider the following trade-off. At each step, we need to make reasonable progress downhill, but do not want to spend too much time choosing the exactly optimal distance to move along the gradient, since the point will only be abandoned at the next iteration anyway. Usually it is best to try and choose the step length \(\alpha\) so that \(f(\boldsymbol{\theta}^{[k]}+\alpha \boldsymbol{\Delta})\) is sufficiently lower than \(f(\boldsymbol{\theta}^{[k]})\), and also so that the magnitude of the gradient of \(f\) in the \(\boldsymbol{\Delta}\) direction is sufficiently reduced by the step. See, e.g., Section 3.1 of Nocedal and Wright (2006) for further details but, for the moment, assume that we have a step selection method.
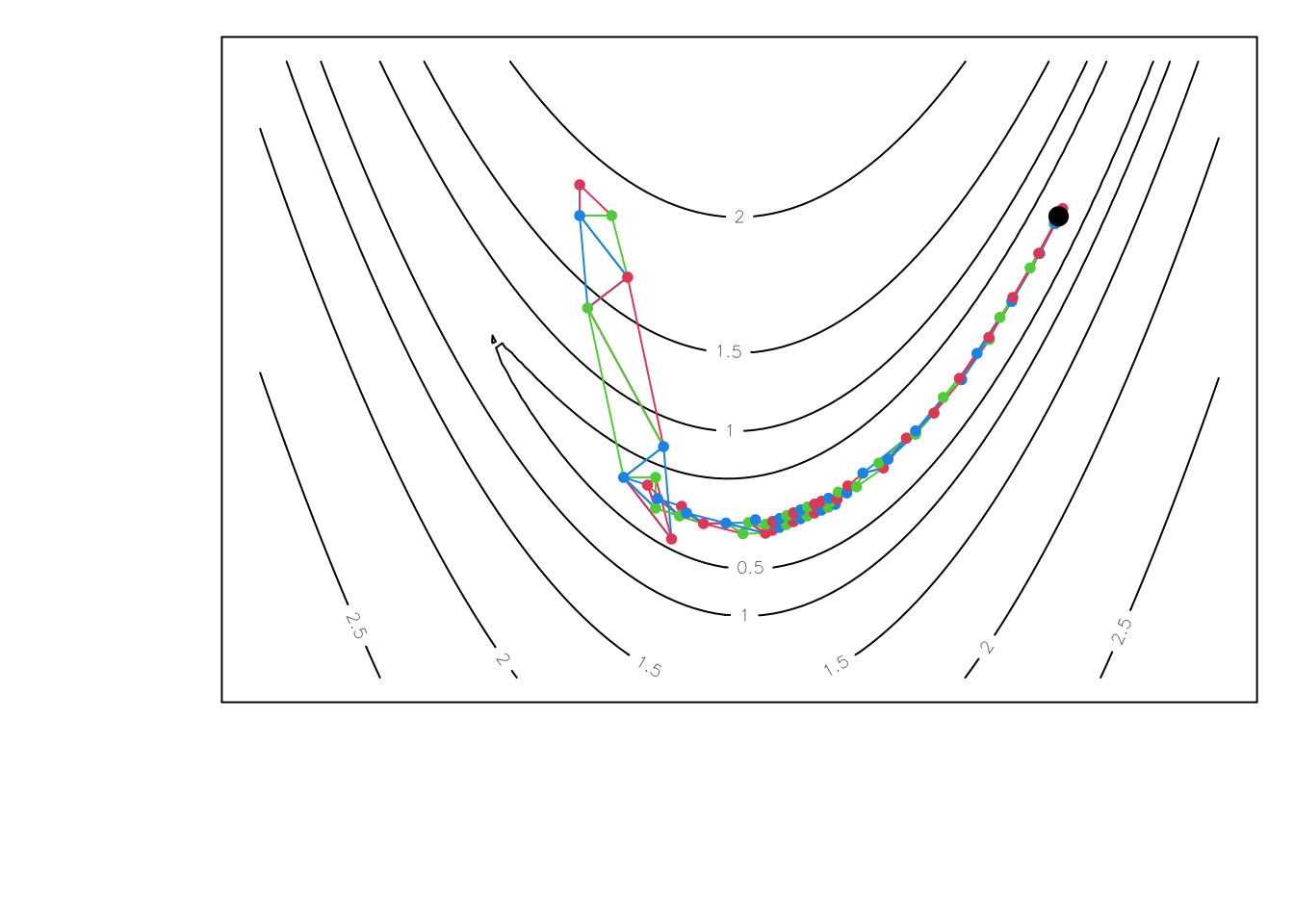
The following illustrates the progress of the steepest descent method on Rosenbrock’s function. The contours are \(\log_{10}\) of Rosenbrock’s function, and the thick line shows the path of the algorithm.

It took 14,845 steps to reach the minimum (the black dot). This excruciatingly slow progress is typical of the steepest descent method, which tends zig-zag when moving across narrow valleys in the objective and to slow down as we approach the minimum, because the gradient is going to zero . Another disadvantage of steepest descent is scale dependence. For simplicity, assume that the arguments \(x\) and \(z\) of the Rosenbrock function above were measured in meters that the we are updating using \[ f(y^{[k+1]}, z^{[k+1]}) = f(y^{[k]}, z^{[k]}) - \alpha \nabla f(y^{[k]}, z^{[k]}), \] with \(\alpha\) being fixed to some small positive constant. Now, imagine that we write an new version of the function, which takes as inputs \(\tilde{x} = x10^3\) and \(\tilde{z} = z10^3\), now measured in kilometers. By the chain rule \(\partial f(\tilde{x}, \tilde{z}) / \partial \tilde{x} = 10^3 \partial f(x, z) / \partial x\) (same for \(\tilde{z}\)), so the proposed steepest descent step is \(10^3\) times larger when the problem is expressed in km. But the range of the axes on the plot above is \(10^3\) times smaller, so the proposed gradient descent steps are massive when working in km and, to obtain an optimisation path that looks the same as above (but with rescaled axes), we would need to divide \(\alpha\) by \(10^6\). Having to adjust the settings of the algorithm depending on the scale being used is annoying enough, but imagine having to optimise \(f(x, \tilde{z})\), that is an objective where the inputs are on very different scales. Now steepest descent takes steps that are much bolder along one direction than along another, and simply adjusting \(\alpha\) is not enough to have a optimisation path that is scale invariant. By contrast, the methods considered in the subsequent sections are scale invariant.
While steepest descent performs poorly for fully optimizing an objective function (i.e. to reach the minimum), a variant of it has become the method of choice in machine learning applications in which we care only about achieving an acceptably low value for an objective which may not even have a unique minimum (e.g. in deep learning). Stochastic gradient descent is useful when the objective function is the sum over broadly equivalent contributions from a large number of data. At each step the negative gradient of the objective for some small, step specific, random sample of the data is obtained, and used as the descent direction for that step. Typically the step length is simply fixed at a small value (which may decrease with iteration). The method is especially interesting when fitting massively over-parameterized models, due to its intrinsic tendency to avoid solutions provide a perfect fit to the training data, but that generalise poorly to test data.
4.3 Newton’s method
As steepest descent approaches the minimum, the first derivative term retained in the Taylor approximation of \(f\) becomes negligible relative to the neglected second derivative term. This largely explains the method’s poor performance. Retaining the second derivative term in the Taylor expansion yields the method of choice for a wide range of problems: Newton’s method. For small \(\boldsymbol{\Delta}\), Taylor’s theorem implies that \[
f(\boldsymbol{\theta}^{[k]} + \boldsymbol{\Delta}) \simeq f(\boldsymbol{\theta}^{[k]}) + \nabla f(\boldsymbol{\theta}^{[k]}) ^{\sf T}\boldsymbol{\Delta} + \frac{1}{2} \boldsymbol{\Delta} ^{\sf T}\nabla^2 f(\boldsymbol{\theta}^{[k]}) \boldsymbol{\Delta}.
\] Differentiating the r.h.s. w.r.t. \(\boldsymbol{\Delta}\) and setting the result to \(\bf 0\) we have \[
\nabla^2 f(\boldsymbol{\theta}^{[k]}) \boldsymbol{\Delta} = - \nabla f(\boldsymbol{\theta}^{[k]})
\tag{3}\]
and, solving the equation for \(\boldsymbol{\Delta}\), leads to the step \[
\boldsymbol{\Delta} = - \left\{ \nabla^2 f(\boldsymbol{\theta}^{[k]}) \right\}^{-1} \nabla f(\boldsymbol{\theta}^{[k]}),
\] which will take us to the turning point of the (quadratic) Taylor approximation of \(f\) (NOTE: we generally do not need to compute the inverse of \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\) to find \(\boldsymbol{\Delta}\), see the matrix computation chapter). This turning point will be a minimum (of the approximation) if \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\) is positive definite.
Notice how Newton’s method automatically suggests a search direction and a step length. Usually we simply accept the Newton step, that we step from \(f(\boldsymbol{\theta}^{[k]})\) to \(f(\boldsymbol{\theta}^{[k]} + \alpha \boldsymbol{\Delta})\), with \(\alpha = 1\) and \(\boldsymbol{\Delta}\) defined as above, unless that step fails to lead to a sufficient decrease in \(f\). In the latter case the step length \(\alpha\) is repeatedly halved until sufficient decrease is achieved.
The second practical issue with Newton’s method is the requirement that \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\) is positive definite. There is no guarantee that it will be, especially if \(\boldsymbol{\theta}^{[k]}\) is far from the optimum. This would be a major problem, were it not for the fact that the solution to \[ {\bf H} \boldsymbol{\Delta} = - \nabla f(\boldsymbol{\theta}^{[k]}) \] is a descent direction for any positive definite \({\bf H}\). To see this, plug \(\boldsymbol{\Delta} = -{\bf H}^{-1}\nabla f(\boldsymbol{\theta}^{[k]})\) into our first-order approximation, \[\begin{align*} f(\boldsymbol{\theta} + \alpha\boldsymbol{\Delta}) &\simeq f(\boldsymbol{\theta}) + \alpha\nabla f({\boldsymbol{\theta}})^{\sf T}{\boldsymbol{\Delta}} \\ &= f({\boldsymbol{\theta}}) - \alpha\nabla f({\boldsymbol{\theta}})^{\sf T}{\bf H}^{-1} \nabla f(\boldsymbol{\theta}) \\ &< f({\boldsymbol{\theta}}), \end{align*}\] for small \(\alpha>0\) due to the positive-definiteness of \({\bf H}^{-1}\).
This gives us the freedom to modify \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\) to make it positive definite, and still be guaranteed a descent direction. One approach is to take the symmetric eigen-decomposition of \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\), reverse the sign of any negative eigenvalues, replace any zero eigenvalues with a small positive number and then replace \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\) by the matrix with this modified eigen-decomposition. Computationally cheaper alternatives simply add a multiple of the identity matrix to \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\), sufficiently large to make the result positive definite. Note that steepest descent corresponds to the choice \({\bf H} = {\bf I}\), and so inflating the diagonal of the Hessian corresponds to nudging the search direction from that of the Newton method towards that of steepest descent, and this is usually a fairly safe and conservative thing to do.
Combining these steps gives a practical Newton algorithm. Starting with \(k=0\) and an initial point \(\boldsymbol{\theta}^{[0]}\), iteratively:
evaluate \(f({\boldsymbol{\theta}^{[k]}})\), \(\nabla f(\boldsymbol{\theta}^{[k]})\) and \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\), implying a quadratic approximation to \(f\), via Taylor’s theorem.
Test whether \(\boldsymbol{\theta}^{[k]}\) is a minimum, and terminate if it is.
If \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\) is not positive definite, perturb it so that it is (thereby modifying the quadratic model of \(f\)).
The search direction \(\boldsymbol{\Delta}\) is now defined by the solution to \[ \nabla^2 f(\boldsymbol{\theta}^{[k]}) \boldsymbol{\Delta} = - \nabla f(\boldsymbol{\theta}^{[k]}), \] i.e. the \(\boldsymbol{\Delta}\) minimising the current quadratic model.
If \(f(\boldsymbol{\theta}^{[k]}+\boldsymbol{\Delta})\) is not sufficiently lower than \(f(\boldsymbol{\theta}^{[k]})\), repeatedly halve \(\boldsymbol{\Delta}\) until it is.
Set \(\boldsymbol{\theta}^{[k+1]} = \boldsymbol{\theta}^{[k]}+\boldsymbol{\Delta}\), increment \(k\) by one and return to step 1.
The following figure illustrates the progress of the method on Rosenbrock’s function, working across rows from top left. Grey contours show the function, dotted show the quadratic approximation at the current best point, and, if present, black contours are the quadratic approximation before modification of the Hessian. The thick black line tracks the steps accepted, while the thin black line shows any suggested steps that were reduced. Note the fact that the method converged in 20 steps, compared to the 14,845 steps taken by steepest descent.
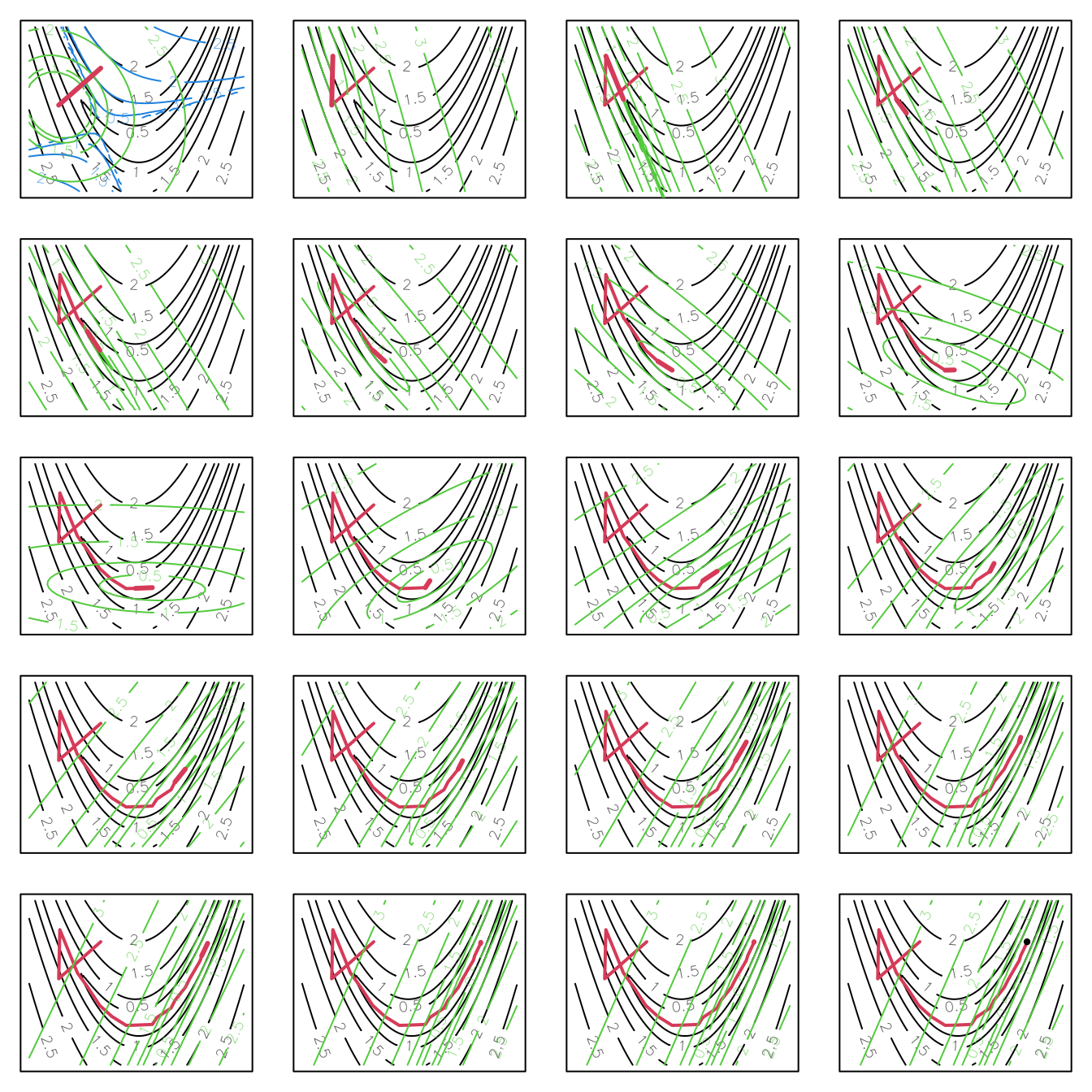
4.4 Quasi-Newton methods
Newton’s method usually performs very well, especially near the optimum, but to use it we require the second derivative (Hessian) matrix of the objective. This can be tedious to obtain. Furthermore, if the dimension of \(\boldsymbol{\theta}\) is large, then solving for the Newton direction can be a substantial part of the computational burden of optimization. Is it possible to produce methods that only require first derivative information, but with efficiency rivalling Newton’s method, rather than steepest descent?
The answer is yes. One approach is to replace the exact Hessian, of Newton’s method, with an approximate Hessian based on finite differences of gradients. The finite difference intervals must be chosen with care (see this), but the approach is reliable (recall that any positive definite matrix in place of the Hessian will yield a descent direction, so using an approximate Hessian should be unproblematic). However, finite differencing for the Hessian is often more costly than exact Hessian evaluation, and solving Equation 3 for \(\boldsymbol \Delta\) can still be expensive (e.g., it might involve computing the Cholesky decomposition of the Hessian, see the matrix chapter).
The second approach is to use a quasi-Newton method. The basic idea is to use first derivative information gathered from past steps of the algorithm to accumulate an approximation to the Hessian at the current best point. In principle, this approximation can be used exactly like the exact Hessian in Newton’s method, but if structured carefully, such an algorithm can also work directly on an approximation to the inverse of the Hessian, thereby reducing the cost of calculating the actual step. It is also possible to ensure that the approximate Hessian is always positive definite.
Quasi-Newton methods were invented in the mid 1950’s by W.C. Davidon (a physicist). In the mathematical equivalent of not signing the Beatles, his paper on the method was rejected (it was eventually published in 1991). There are now many varieties of Quasi-Newton method, but the most popular is the BFGS method, which will be briefly covered here. BFGS is named after Broyden, Fletcher, Goldfarb and Shanno all of whom independently discovered and published it, around 1970.
We suppose that at step \(k\) we have already computed \(\boldsymbol{\theta}^{[k]}\) and a positive definite approximate Hessian \({\bf H}^{[k]}\), with inverse \({\bf B}^{[k]}\). So, just as with a regular Newton method, the trial update step is \[ {\boldsymbol{\Delta}} = - {\bf B}^{[k]} \nabla f({\boldsymbol{\theta}}^{[k]}), \] leading either to a new \(\boldsymbol{\theta}^{[k+1]}\) directly, or more likely via line search. We now have the problem of how to appropriately update the approximate Hessian, \({\bf H}^{[k+1]}\) or, better still, its inverse. We want the approximate Hessian to stay positive definite and to give us a good quadratic approximation of our function about \(\boldsymbol{\theta}^{[k+1]}\). If \({\bf H}^{[k+1]}\) is our new approximate Hessian at the \((k+1)^{\rm th}\) step, we have the function approximation \[ f(\boldsymbol{\theta}) \simeq f(\boldsymbol{\theta}^{[k+1]}) + \nabla f(\boldsymbol{\theta}^{[k+1]})^{\sf T}(\boldsymbol{\theta} - {\boldsymbol{\theta}^{[k+1]}}) + \frac{1}{2} (\boldsymbol{\theta} - {\boldsymbol{\theta}^{[k+1]}})^{\sf T}{\bf H}^{[k+1]} (\boldsymbol{\theta} - {\boldsymbol{\theta}^{[k+1]}}). \] around \(\boldsymbol{\theta}^{[k+1]}\). The basic requirement of a quasi Newton method is that the new Hessian should be a modification of the old Hessian chosen so that the approximation should exactly match \(\nabla f(\boldsymbol{\theta}^{[k]})\) — i.e. the approximation should get the gradient vector at the previous best point, \(\boldsymbol{\theta}^{[k]}\), exactly right. In particular, let us that the gradient of the above approximation w.r.t. \(\boldsymbol \theta\) to obtain \[ \nabla f({\boldsymbol{\theta}}) \simeq \nabla f(\boldsymbol{\theta}^{[k+1]}) + {\bf H}^{[k+1]}({\boldsymbol{\theta}}-{\boldsymbol{\theta}}^{[k+1]}). \] Then, evaluating this at \({\boldsymbol{\theta}}^{[k]}\) leads to our requirement \[ \nabla f(\boldsymbol{\theta}^{[k]})= \nabla f(\boldsymbol{\theta}^{[k+1]}) + {\bf H}^{[k+1]} (\boldsymbol{\theta}^{[k]} - {\boldsymbol{\theta}^{[k+1]}}), \] which can be seen as a first order Taylor expansion of the gradient function, centered at \(\boldsymbol{\theta}^{[k+1]}\) and evaluated at \(\boldsymbol{\theta}^{[k]}\).
The requirement can be written \[ {\bf H}^{[k+1]} {\bf s}_k = {\bf y}_k \;\;\text{ or, equivalently, } \;\; {\bf B}^{[k+1]} {\bf y}_k = {\bf s}_k \tag{4}\] where \({\bf s}_k = \boldsymbol{\theta}^{[k+1]} - \boldsymbol{\theta}^{[k]}\) and \({\bf y}_k = \nabla f(\boldsymbol{\theta}^{[k+1]}) - \nabla f(\boldsymbol{\theta}^{[k]})\). The so-called secant equation (Equation 4) will only be feasible if \({\bf s}_k^{\sf T}{\bf y}_k>0\), because positive definiteness of \({\bf H}^{[k+1]}\) implies that the l.h.s. of \({\bf s}_k^{\sf T}{\bf H}^{[k+1]} {\bf s}_k = {\bf s}_k^{\sf T}{\bf y}_k\) must be positive. Later we will need to choose the step length appropriately to guarantee this.
Now consider how to ensure that Equation 4 will be be true, by applying low rank modifications to \({\bf B}^{[k]}\), until the modified matrix multiplied by \({\bf y}_k\) equals \({\bf s}_k\). Defining \(\rho_k = ({\bf s}_k^{\sf T}{\bf y}_k)^{-1}\) let’s start with a rank one update designed to cancel \({\bf B}^{[k]} {\bf y}_k\) \[ {\bf B}^{[k]} - \rho_k {\bf B}^{[k]}{\bf y}_k {\bf s}_k ^{\sf T}~~ \Rightarrow ~~ {\bf B}^{[k]}{\bf y}_k - \rho_k {\bf B}^{[k]}{\bf y}_k {\bf s}_k ^{\sf T}{\bf y}_k = {\bf 0} \] That update is not symmetric, but if we re-write it as \({\bf B}^{[k]}({\bf I} - \rho_k {\bf y}_k {\bf s}_k^{\sf T})\) it is obvious that pre-multiplying by the transpose of the factor in brackets will restore symmetry and that we still have \[ ({\bf I} - \rho_k {\bf s}_k{\bf y}_k^{\sf T}){\bf B}^{[k]}({\bf I} - \rho_k {\bf y}_k {\bf s}_k^{\sf T}) {\bf y}_k = {\bf 0}. \] Now we just need to add a symmetric low rank update whose product with \({\bf y}_k\) is \({\bf s}_k\), and obviously \(\rho_k {\bf s}_k{\bf s}_k^{\sf T}\) does the job. That is \[ {\bf B}^{[k+1]} = ({\bf I} - \rho_k {\bf s}_k {\bf y}_k^{\sf T}) {\bf B}^{[k]} ({\bf I} - \rho_k {\bf y}_k {\bf s}_k^{\sf T}) + \rho_k {\bf s}_k {\bf s}_k^{\sf T}, \] from which it is obvious that \({\bf B}^{[k+1]}\) is positive definite if \(\rho_k>0\), equivalently \({\bf s}_k^{\sf T}{\bf y}_k>0\). Note that, when using this update, we obviously do not explicitly form \(({\bf I} - \rho_k {\bf y}_k {\bf s}_k^{\sf T})\), but expand the expression to obtain a form computable at \(O(p^2)\) cost, where \(p\) is the dimension.
This \(\rho_k>0\) condition can be met by choosing the step length to ensure not only that the objective decreases sufficiently, but also that the magnitude of the gradient reduces sufficiently. Specifically choosing the constants \(c_1 \in (0,1)\) and \(c_2 \in (c_1, 1)\) (\(10^{-4}\) and 0.9 are typical), then the length of step \(\boldsymbol{\Delta}\) is chosen to satisfy the Wolfe conditions
- \(f({\boldsymbol{\theta}}^{[k]}+\Delta) \le f({\boldsymbol{\theta}}^{[k]}) + c_1 \nabla f({\boldsymbol{\theta}}^{[k]}) ^{\sf T}\boldsymbol{\Delta}\) (sufficient decrease)
- \(\nabla f({\boldsymbol{\theta}}^{[k]}+\Delta)^{\sf T}\Delta \ge c_2 \nabla f({\boldsymbol{\theta}}^{[k]})^{\sf T}\Delta\) (curvature).
This is always possible (Nocedal & Wright, 2006, Section 3.5). Also, from the second condition we have \[ [\nabla f({\boldsymbol{\theta}}^{[k]}+\Delta)-\nabla f({\boldsymbol{\theta}}^{[k]})]^{\sf T}\Delta \ge (c_2-1) \nabla f({\boldsymbol{\theta}}^{[k]})^{\sf T}\Delta \] The l.h.s. is simply \({\bf y}_k^{\sf T}{\bf s}_k\), while the right hand side is positive since \(\nabla f({\boldsymbol{\theta}}^{[k]})^{\sf T} \Delta\) is negative by the definition of \(\boldsymbol{\Delta}\) and positive definiteness of \({\bf B}^{[k]}\). Hence the second Wolfe condition guarantees that \({\bf y}_k^{\sf T}{\bf s}_k>0\) and \({\bf B}^{[k+1]}\) is positive definite.
Apart from the more careful step length selection, the BFGS method then works exactly like Newton’s method, but with \({\bf B}^{[k]}\) in place of the inverse of \(\nabla^2 f(\boldsymbol{\theta}^{[k]})\), and without the need for second derivative evaluation or for perturbing the (inverse) Hessian to achieve positive definiteness. Notice how if \(p=\text{dim}(\boldsymbol{\theta})\) the update to \({\bf B}^{[k+1]}\) and computation of the step \(\boldsymbol{\Delta}\) are \(O(p^2)\), compared to the \(O(p^3)\) of Newton’s method. A finite difference approximation to the Hessian is often used to initialise \({\bf B}^{[0]}\), which otherwise can be set to the identity matrix multiplied by a suitable constant.
Given that Equation 4 supplies \(p\) constraints, but the inverse Hessian has \(p(p+1)/2\) elements to update, the BFGS update derived above is obviously not the only possibility. For example we could have insisted on using a rank one update (BFGS’s update is rank two), in which case there is only one possibility if the \({\bf B}\) is to stay symmetric, however this Symmetric Rank 1 (SR1) update does not tend to work as well as BFGS in practice. Another possibility would have been to apply exactly the same process applied above to the \({\bf H}^{[k+1]} {\bf s}_k = {\bf y}_k\) version of the secant equation. That leads to updates for \({\bf H}^{[k]}\) which have the same form as the \({\bf B}^{[k]}\) updates, but with \({\bf y}_k\) and \({\bf s}_k\) swapping places. This was actually Davidon’s original proposal. There are many other possibilities, and much theoretical work on the update properties (see Nocedal & Wright, 2006), but in practice the BFGS seems to work best in most cases.
A notable variant is the limited memory version of the algorithm (L-BFGS, see Nocedal & Wright, 2006, Section 7.2), which reduces the \(O(p^2)\) cost of storing and computing with \({\bf B}^{[k]}\) to \(O(kp)\) by maintaining only a rank \(k \ll p\) approximation to \({\bf B}^{[k]}\). The main advantage of this is to save memory when \(p\) is very large. The operations cost reduction is less clear cut: what is gained in operations cost reduction per step is often lost because more steps are required.
The following figure illustrates the application of BFGS. Notice how this quasi-Newton method has taken nearly twice as many steps (38) as the Newton method (20), for the same problem, and shows a greater tendency to ‘zig-zag’. However, it is still computationally cheaper than finite differencing for the Hessian, which would have required an extra 20 gradient evaluations, compared to quasi-Newton. Compared to steepest descent it’s miraculous.
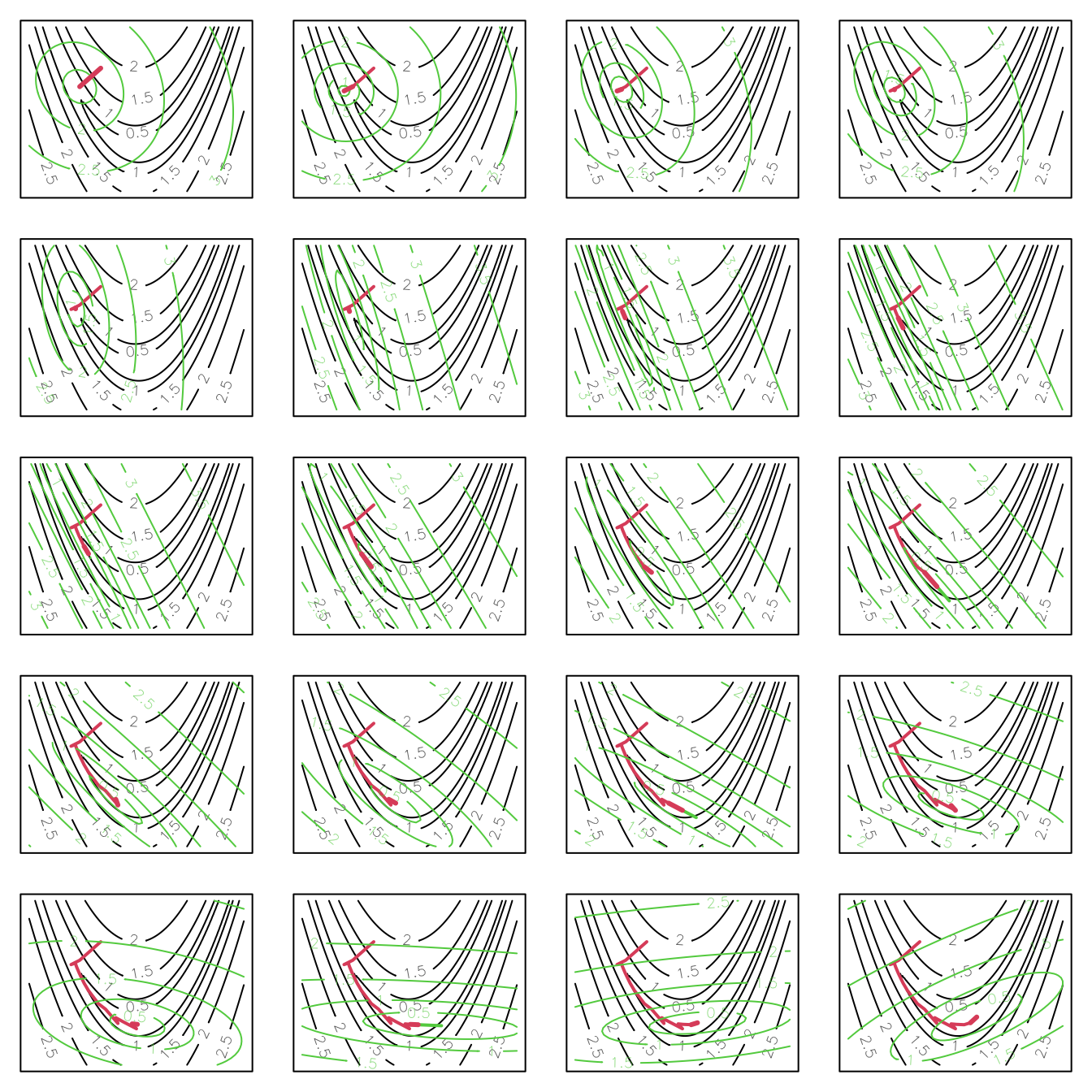
4.5 The Nelder–Mead polytope method
What if even gradient evaluation is too taxing, or if our objective is not smooth enough for Taylor approximations to be valid (or perhaps even possible)? What can be done with function values alone? The Nelder–Mead polytope (also known as the downhill simplex method, which should not be confused with the completely different simplex method of linear programming) method provides a rather successful answer, and as with the other methods we have met, it is beautifully simple.
Let \(n\) be the dimension of \(\boldsymbol{\theta}\). At each stage of the method we maintain \(n+1\) distinct \(\boldsymbol{\theta}\) vectors, defining a polytope in \(\Theta\) (e.g. for a 2-dimensional \(\boldsymbol{\theta}\), the polytope is a triangle). The following is iterated until a minimum is reached (indicated by the polytope collapsing to a point).
- The search direction is defined as the vector from the worst point (vertex of the polytope with highest objective value) through the average (the centroid) of the remaining \(n\) points.
- The initial step length is set to twice the distance from the worst point to the centroid of the others. If it succeeds (meaning that the new point is no longer the worst point) then a step length of 1.5 times that is tried, and the better of the two accepted, replacing the worst point.
- If the previous step did not find a successful new point then step lengths of half and one and a half times the distance from the worst point to the centroid are tried. If one reduces the objective then the better of the 2 replaces the worst point.
- If the last two steps failed to locate a successful point then the polytope is reduced in size, by linear rescaling towards the current best point (which remains fixed.)
Variations are possible, in particular with regard to the step lengths and shrinkage factors.
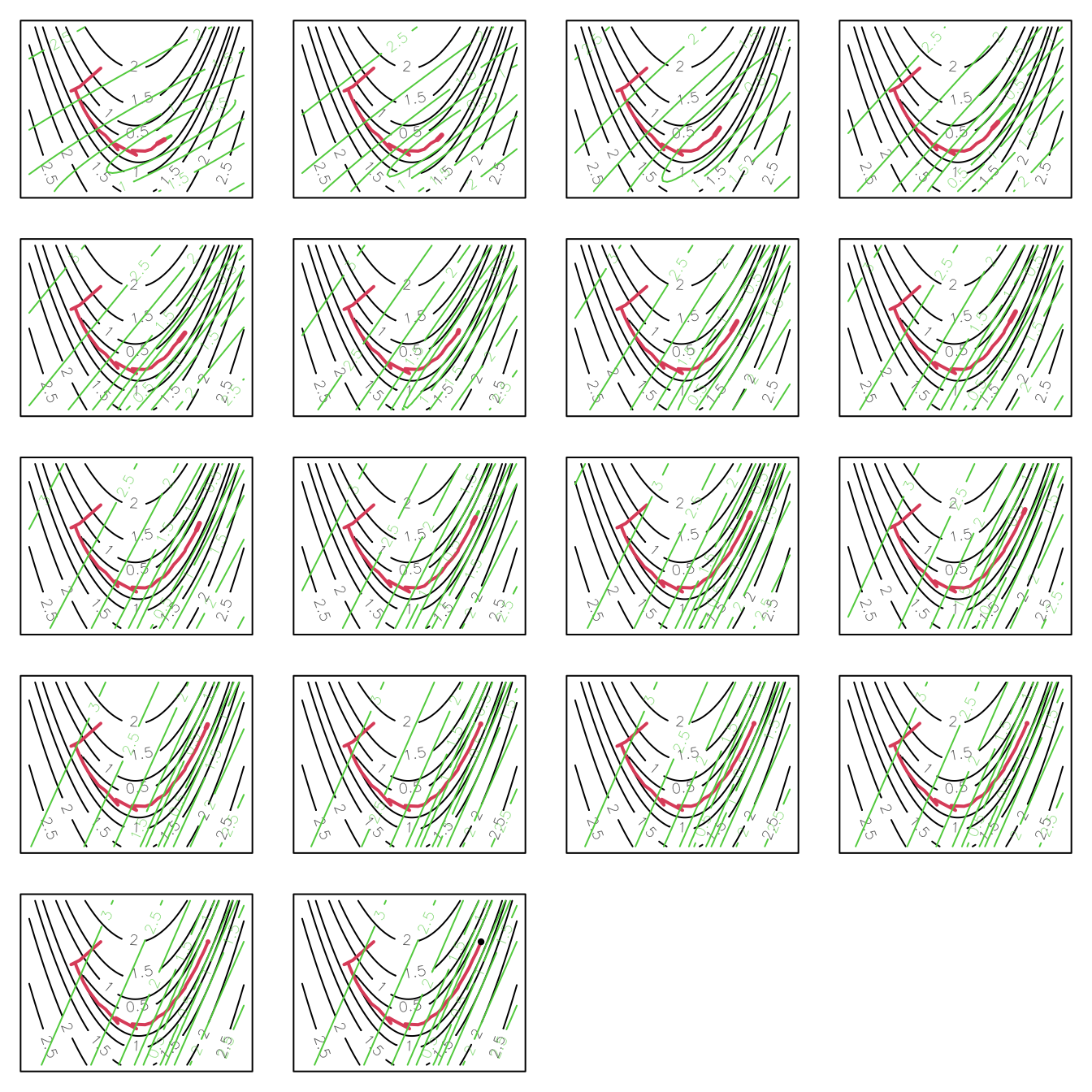
The following figure illustrates the polytope method in action. Each polytope is plotted, with the line style cycling through, black, grey and dashed black. The worst point in each polytope is highlighted with a circle.
In this case it took 79 steps to reach the minimum of Rosenbrock’s function. This is somewhat more than Newton or BFGS, but given that we need no derivatives in this case, the amount of computation is actually less.
On the basis of this example you might be tempted to suppose that Nelder-Mead is all you ever need, but this is generally not the case. If you need to know the optimum very accurately then Nelder-Mead will often take a long time to get an answer that Newton based methods would give very quickly. Also, the polytope can get ‘stuck’, so that it is usually a good idea to restart the optimization from any apparent minimum (with a new polytope having the apparent optimum as one vertex), to check that further progress is really not possible. Essentially, Nelder-Mead is good if the answer does not need to be too accurate, and derivatives are hard to come by, but you wouldn’t use it as the underlying optimizer for general purpose modelling software, for example.
4.6 Other methods
These notes can only provide a brief overview of some important methods. There are many other optimization methods, and quite a few are actually useful. For example:
In likelihood maximisation contexts the method of scoring or Fisher’s scoring is often used. Here the Hessian in Newton’s method is replaced with the expected Hessian (i.e., the Fisher information matrix).
The Gauss-Newton method is another way of getting a Newton type method when only first derivatives are available. It is applicable when the objective is somehow related to a sum of squares of differences between some data and the model predictions of those data, and has a nice interpretation in terms of approximating linear models. It is closely related to the algorithm for fitting Generalized Linear Models.
Conjugate gradient methods are another way of getting a good method using only first derivative information. The problem with steepest descent is that if you minimise along one steepest descent direction then the next search direction is always at right angles to it. This can mean that it takes a huge number of tiny zig-zagging steps to minimise even a perfectly quadratic function. If \(n\) is the dimension of \(\boldsymbol{\theta}\), then Conjugate Gradient methods aim to construct a set of \(n\) consecutive search directions such that successively minimising along each will lead you exactly to the minimum of a quadratic function.
Simulated annealing is a gradient-free method for optimizing difficult objectives, such as those arising in discrete optimization problems, or with very spiky objective functions. The basic idea is to propose random changes to \(\boldsymbol{\theta}\), always accepting a change which reduces \(f(\boldsymbol{\theta})\), but also accepting moves which increase the objective, with a probability which decreases with the size of increase, and also decreases as the optimization progresses.
The EM algorithm is a useful approach to likelihood maximisation when there are missing data or random effects that are difficult to integrate out.
5 Constrained optimization
Sometimes optimization must be performed subject to constraints on \(\boldsymbol{\theta}\). An obvious way to deal with constraints is to re-parameterise to arrive at an unconstrained problem. For example if \(\theta_1 > 0\) we might choose to work in terms of the unconstrained \(\theta^\prime_1\) where \(\theta_1 = \exp(\theta_1^\prime)\), and more complicated re-parameterisations can impose quite complex constraints in this way. While often effective re-parameterisation suffers from at least three problems:
It is not possible for all constraints that might be required.
The objective is sometimes a more awkward function of the new parameters than it was of the old.
There can be problems with the unconstrained parameter estimates tending to \(\pm \infty\). For example if \(\theta_1\) above is best estimated to be zero then the best estimate of \(\theta^\prime_1\) is \(- \infty\).
A second method is to add to the objective function a penalty function penalising violation of the constraints. The strength of such a penalty has to be carefully chosen, and of course the potential to make the objective more awkward than the original applies here too.
The final set of approaches treat the constraints directly. For linear equality and inequality constraints constrained Newton type methods are based on the methods of quadratic programming. Non-linear constraints are more difficult, but can often be discretised into a set of approximate linear constraints.
6 Modifying the objective
If you have problems optimizing an objective function, then sometimes it helps to modify the function itself. For example:
Reparameterisation can turn a very unpleasant function into something much easier to work with (e.g. it is often better to work with precision than with standard deviation when dealing with normal likelihoods).
Transform the objective. e.g. \(\log(f)\) will be ‘more convex’ than \(f\): this is usually a good thing.
Consider perturbing the data. For example an objective based on a small sub sample of the data can sometimes be a good way of finding starting values for the full optimization. Similarly resampling the data can provide a means for escaping small scale local minima in an objective if the re-sample based objective is alternated with the true objective as optimization progresses, or if the objective is averaged over multiple re-samples. cf. SGD.
Sometimes a problem with optimization indicates that the objective is not a sensible one. e.g. in the third example in Section 3, an objective based on getting the observed ACF right makes more sense, and is much better behaved.
7 Software
R includes a routine optim for general purpose optimization by BFGS, Nelder-Mead, Conjugate Gradient or Simulated Annealing. The R routine nlm uses Newton’s method and will use careful finite difference approximations for derivatives which you don’t supply. R has a number of add on packages e.g. quadprog, linprog, trust to name but 3. See NEOS Guide for a really useful guide to what is more generally available.
Should you ever implement your own optimization code? Many people reply with a stern ‘no’, but I am less sure. For the methods presented in detail above, the advantages of using your own implementation are (i) the un-rivalled access to diagnostic information and (ii) the knowledge of exactly what the routine is doing. However, if you do go down this route it is very important to read further about step length selection and termination criteria. Where greater caution is needed is if you require constrained optimization, large scale optimization or to optimize based on approximate derivatives. All these areas require careful treatment.
8 Further reading on optimization
Nocedal and Wright (2006) Numerical Optimization 2nd ed. Springer, is a very clear and up to date text. If you are only going to look at one text, then this is probably the one to go for.
Gill, P.E. , W. Murray and M.H. Wright (1981) Practical Optimization Academic Press, is a classic, particularly on constrained optimization. I’ve used it to successfully implement quadratic programming routines.
Dennis, J.E. and R.B. Schnabel (1983) Numerical Methods for Unconstrained Optimization and Nonlinear Equations (re-published by SIAM, 1996), is a widely used monograph on unconstrained methods (the
nlmroutine in R is based on this one).Press WH, SA Teukolsky, WT Vetterling and BP Flannery (2007) Numerical Recipes (3rd ed.), Cambridge and Monahan, JF (2001) Numerical Methods of Statistics, Cambridge, both discuss Optimization at a more introductory level.